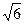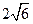题目内容
已知抛物线C:x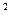 =2py(
=2py( p>0)上一点A(m,4)到其焦点的距离为
p>0)上一点A(m,4)到其焦点的距离为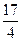 .
.
(Ⅰ)求p和m的值;
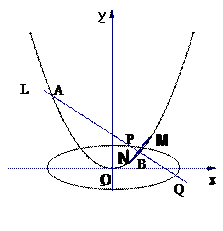
(Ⅱ)设B(-1,1),过点B任作两直线A1B1,A2B2,与抛物线C分别交于点A1,B1,A2,B2,过A1,B1的抛物线C的两切线交于P,过A2,B2的抛物线C的两切线交于Q,求PQ的直线方程.
 =2py(
=2py( p>0)上一点A(m,4)到其焦点的距离为
p>0)上一点A(m,4)到其焦点的距离为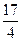 .
.(Ⅰ)求p和m的值;
(Ⅱ)设B(-1,1),过点B任作两直线A1B1,A2B2,与抛物线C分别交于点A1,B1,A2,B2,过A1,B1的抛物线C的两切线交于P,过A2,B2的抛物线C的两切线交于Q,求PQ的直线方程.
解:(Ⅰ)由抛物线方程得其准线方程: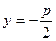 ,
, 根据抛物线定义
根据抛物线定义
点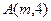 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即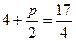 ,解得
,解得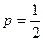
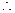 抛物线方程为:
抛物线方程为: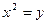 ,将
,将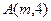 代入抛物线方程,解得
代入抛物线方程,解得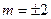 ………6分
………6分
(Ⅱ)因为点B(-1,1) 在抛物线C上,所以B1,B2即为点B,
则过A1,B1的抛物线C的两切线交于P在过B的抛物线C的切线上,
过A2,B 2的抛物线C的两切线交于Q同样在过B的抛
2的抛物线C的两切线交于Q同样在过B的抛 物线C的切线上,
物线C的切线上,
故直线PQ就是抛物线C在点B(-1,1)处的切线,易求其直线方程为y=―2x―1 15分
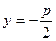 ,
, 根据抛物线定义
根据抛物线定义点
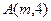 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即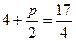 ,解得
,解得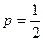
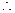 抛物线方程为:
抛物线方程为: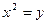 ,将
,将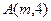 代入抛物线方程,解得
代入抛物线方程,解得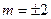 ………6分
………6分(Ⅱ)因为点B(-1,1) 在抛物线C上,所以B1,B2即为点B,
则过A1,B1的抛物线C的两切线交于P在过B的抛物线C的切线上,
过A2,B
 2的抛物线C的两切线交于Q同样在过B的抛
2的抛物线C的两切线交于Q同样在过B的抛 物线C的切线上,
物线C的切线上,故直线PQ就是抛物线C在点B(-1,1)处的切线,易求其直线方程为y=―2x―1 15分
略

练习册系列答案
相关题目
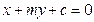 与抛物线
与抛物线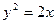 交于A、B两点,O点是坐标原点。
交于A、B两点,O点是坐标原点。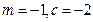 时,求证:OA⊥OB;
时,求证:OA⊥OB;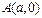 和
和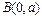 的直线与抛物线
的直线与抛物线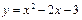 没有交点,那么实数
没有交点,那么实数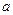 的取值范围是
的取值范围是 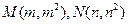 是抛物线
是抛物线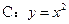 上两个不同点,且
上两个不同点,且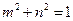 ,
,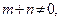 直线
直线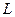 是线段
是线段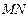 的垂直平分线.设椭圆E的方程为
的垂直平分线.设椭圆E的方程为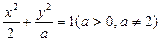 .
.
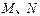 在
在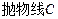 上移动时,求直线
上移动时,求直线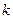 的取值范围;
的取值范围;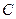 交于A、B两个不同点,
交于A、B两个不同点, 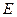 交于P、Q两个不同点,设AB中点为
交于P、Q两个不同点,设AB中点为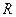 ,
,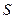 ,若
,若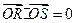 ,求
,求 在交点处的切线方程。
在交点处的切线方程。 知抛物线
知抛物线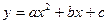 通过点P(1,1),且在点Q(2,-1)处与直线
通过点P(1,1),且在点Q(2,-1)处与直线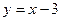 相切,求实数
相切,求实数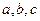 的值.
的值.  时,水面宽4
时,水面宽4