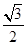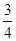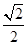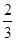题目内容
直线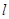 与椭圆
与椭圆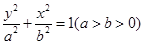 交于
交于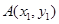 ,
,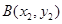 两点,已知
两点,已知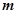
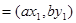 ,
,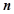
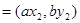 ,若
,若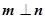 且椭圆的离心率
且椭圆的离心率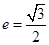 ,又椭圆经过点
,又椭圆经过点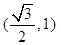 ,
,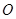 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线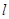 过椭圆的焦点
过椭圆的焦点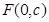 (
(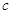 为半焦距),求直线
为半焦距),求直线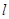 的斜率
的斜率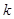 的值;
的值;
(Ⅲ)试问: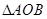 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
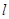 与椭圆
与椭圆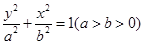 交于
交于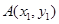 ,
,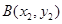 两点,已知
两点,已知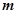
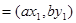 ,
,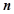
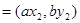 ,若
,若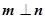 且椭圆的离心率
且椭圆的离心率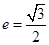 ,又椭圆经过点
,又椭圆经过点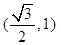 ,
,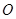 为坐标原点.
为坐标原点.(Ⅰ)求椭圆的方程;
(Ⅱ)若直线
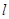 过椭圆的焦点
过椭圆的焦点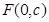 (
(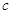 为半焦距),求直线
为半焦距),求直线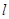 的斜率
的斜率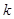 的值;
的值;(Ⅲ)试问:
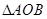 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.(Ⅰ)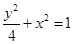 (Ⅱ)
(Ⅱ)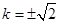 (Ⅲ)三角形的面积为定值。证明见解析
(Ⅲ)三角形的面积为定值。证明见解析
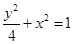 (Ⅱ)
(Ⅱ)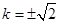 (Ⅲ)三角形的面积为定值。证明见解析
(Ⅲ)三角形的面积为定值。证明见解析(I)由e和椭圆过点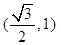 可得到关于a,b的两个方程,从而解出a,b值求出椭圆的方程.
可得到关于a,b的两个方程,从而解出a,b值求出椭圆的方程.
(II) 设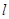 的方程为
的方程为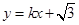 ,由已知
,由已知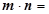
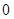 得:
得:
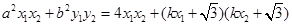
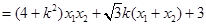 =0,
=0,
然后直线方程与椭圆方程联立消y后得到关于x的一元二次方程,利用韦达定理建立关于k的方程求出k值.
(III)要讨论AB斜率存在与不存在两种情况.研究当AB斜率存在时,由已知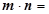
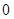 ,得
,得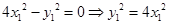 ,又
,又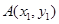 在椭圆上,所以
在椭圆上,所以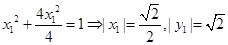 ,从而证明出
,从而证明出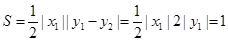 为定值.
为定值.
解:(Ⅰ)∵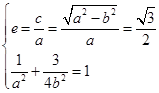 ……2分
……2分
∴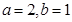
∴椭圆的方程为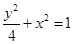 ……………3分
……………3分
(Ⅱ)依题意,设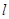 的方程为
的方程为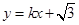
由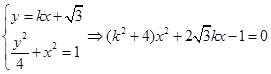
显然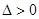
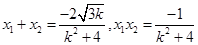 ………………5分
………………5分
由已知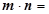
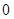 得:
得:
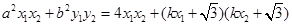
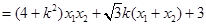
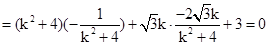
解得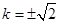 ……………………6分
……………………6分
(Ⅲ)①当直线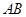 斜率不存在时,即
斜率不存在时,即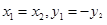 ,
,
由已知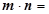
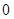 ,得
,得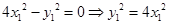
又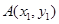 在椭圆上,
在椭圆上,
所以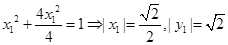
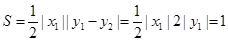 ,三角形的面积为定值.………7分
,三角形的面积为定值.………7分
②当直线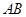 斜率存在时:设
斜率存在时:设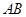 的方程为
的方程为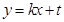
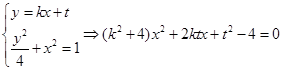
必须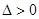 即
即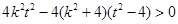
得到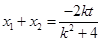 ,
,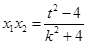 ………………9分
………………9分
∵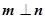 ,∴
,∴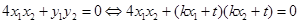
代入整理得: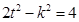 …………………10分
…………………10分
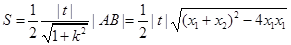 …………11分
…………11分
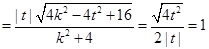 所以三角形的面积为定值. ……12分
所以三角形的面积为定值. ……12分
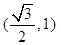 可得到关于a,b的两个方程,从而解出a,b值求出椭圆的方程.
可得到关于a,b的两个方程,从而解出a,b值求出椭圆的方程.(II) 设
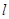 的方程为
的方程为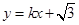 ,由已知
,由已知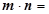
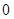 得:
得: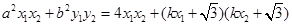
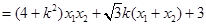 =0,
=0,然后直线方程与椭圆方程联立消y后得到关于x的一元二次方程,利用韦达定理建立关于k的方程求出k值.
(III)要讨论AB斜率存在与不存在两种情况.研究当AB斜率存在时,由已知
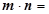
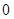 ,得
,得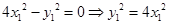 ,又
,又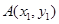 在椭圆上,所以
在椭圆上,所以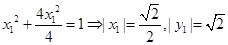 ,从而证明出
,从而证明出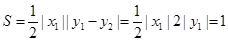 为定值.
为定值.解:(Ⅰ)∵
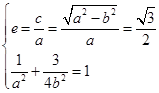 ……2分
……2分∴
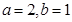
∴椭圆的方程为
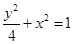 ……………3分
……………3分(Ⅱ)依题意,设
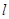 的方程为
的方程为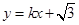
由
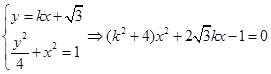
显然
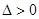
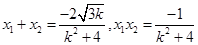 ………………5分
………………5分由已知
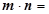
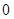 得:
得: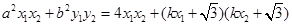
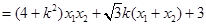
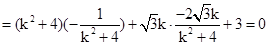
解得
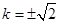 ……………………6分
……………………6分(Ⅲ)①当直线
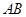 斜率不存在时,即
斜率不存在时,即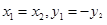 ,
,由已知
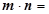
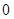 ,得
,得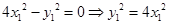
又
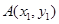 在椭圆上,
在椭圆上,所以
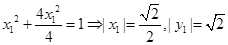
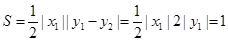 ,三角形的面积为定值.………7分
,三角形的面积为定值.………7分②当直线
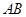 斜率存在时:设
斜率存在时:设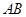 的方程为
的方程为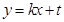
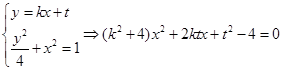
必须
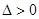 即
即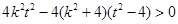
得到
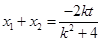 ,
,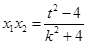 ………………9分
………………9分∵
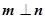 ,∴
,∴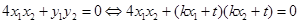
代入整理得:
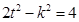 …………………10分
…………………10分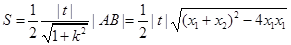 …………11分
…………11分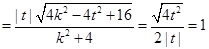 所以三角形的面积为定值. ……12分
所以三角形的面积为定值. ……12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
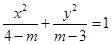 表示焦点在
表示焦点在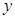 轴上的椭圆,则
轴上的椭圆,则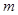 的取值范围是 ( )
的取值范围是 ( )



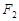 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,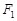 的直线MF1是圆
的直线MF1是圆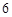 ,离心率
,离心率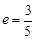 ,焦点在
,焦点在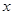 轴上的椭圆标准方程是 ( )
轴上的椭圆标准方程是 ( )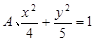
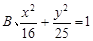
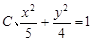
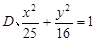
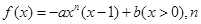 为正整数,
为正整数,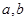 为常数.曲线
为常数.曲线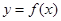 在点
在点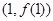 处的切线方程为
处的切线方程为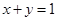 .
.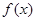 的最大值;
的最大值;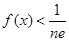 .
.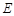 的普通方程为
的普通方程为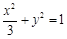
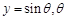 为参数,求椭圆
为参数,求椭圆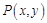 是椭圆
是椭圆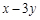 的取值范围.
的取值范围.  过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点, 的最小值为2,则其离心率为( )
的最小值为2,则其离心率为( )

 +
+ =1的离心率 e =
=1的离心率 e = , 则k的值是
, 则k的值是 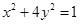 的离心率为( )
的离心率为( )