题目内容
如果方程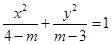 表示焦点在
表示焦点在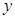 轴上的椭圆,则
轴上的椭圆,则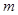 的取值范围是 ( )
的取值范围是 ( )
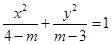 表示焦点在
表示焦点在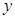 轴上的椭圆,则
轴上的椭圆,则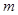 的取值范围是 ( )
的取值范围是 ( )A. | B. | C. | D. |
D
试题分析:由题意可得:方程
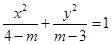 表示焦点在y轴上的椭圆,所以4-m>0,m-3>0并且m-3>4-m,解得:
表示焦点在y轴上的椭圆,所以4-m>0,m-3>0并且m-3>4-m,解得: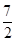 <m<4.故选D.
<m<4.故选D.点评:解决该试题的关键是理解椭圆的焦点位置取决于分母中那个大,则对应的焦点位置在那个轴上来得到。

练习册系列答案
相关题目
题目内容
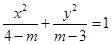 表示焦点在
表示焦点在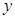 轴上的椭圆,则
轴上的椭圆,则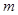 的取值范围是 ( )
的取值范围是 ( )A. | B. | C. | D. |
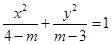 表示焦点在y轴上的椭圆,所以4-m>0,m-3>0并且m-3>4-m,解得:
表示焦点在y轴上的椭圆,所以4-m>0,m-3>0并且m-3>4-m,解得: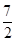 <m<4.故选D.
<m<4.故选D.