题目内容
如图,在 中,点
中,点 在
在 边上,
边上, ,
, ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的面积.
的面积.

 中,点
中,点 在
在 边上,
边上, ,
, ,
, .
.(Ⅰ)求
 的值;
的值;(Ⅱ)求
 的面积.
的面积.
解:(I)由
 ,得
,得 ……………………2分
……………………2分又
 ,则
,则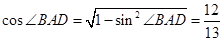 ………………………………4分
………………………………4分故
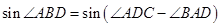

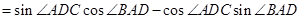
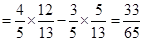 ………………………………………………………7分
………………………………………………………7分(Ⅱ)在△
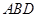 中,由正弦定理知,
中,由正弦定理知,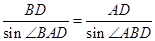 ,
,则
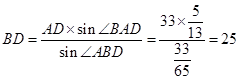 ………………………………………………………11分
………………………………………………………11分故
 的面积为
的面积为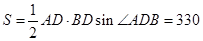 …………………………………………14分
…………………………………………14分略

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为 (如图2)
(如图2) 平面
平面 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 到平面
到平面 的距离.
的距离.

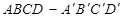 中,
中,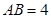 ,
,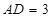 ,
,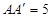 ,
,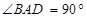 ,
, ,则对角线
,则对角线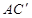 的长度为
的长度为 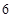
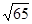
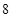
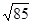
 -
- 中,异面直线
中,异面直线 与
与 所成角的大小为 ▲ ;
所成角的大小为 ▲ ; 中,已知
中,已知 ,
, ,
, .
. 与底面
与底面 所成角正切值;
所成角正切值; (不包含端点)上确定一点
(不包含端点)上确定一点 的位置,
的位置, (要求说明理由);
(要求说明理由); ,求二面角
,求二面角 的大小.
的大小.
 中,
中, ,
, ,点
,点 在
在 上且
上且 (如图(3)).把
(如图(3)).把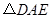 沿
沿 向上折起到
向上折起到 的位置,使二面角
的位置,使二面角 的大小为
的大小为 (如图(4)).
(如图(4)). 的体积;
的体积; 与平面
与平面 所成角的正切值;
所成角的正切值; 为
为 上的点
上的点 ,使
,使 平面
平面
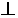 平面ABCD,
平面ABCD,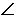 ABC=60O,E,F分别是BC,PC
ABC=60O,E,F分别是BC,PC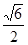 。
。