题目内容
(本小题满分14分)
如图,四边形 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为 (如图2)
(如图2)
(1)求证: 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求点 到平面
到平面 的距离.
的距离.

如图,四边形
 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为 (如图2)
(如图2)(1)求证:
 平面
平面 ;
;(2)求异面直线
 与
与 所成角的余弦值;
所成角的余弦值;(3)求点
 到平面
到平面 的距离.
的距离.
解:
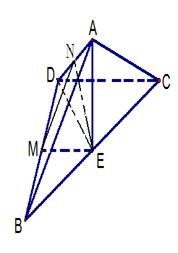
(1)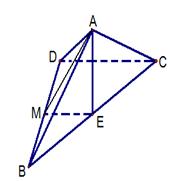 如图取BD中点M,连接AM,ME。因
如图取BD中点M,连接AM,ME。因
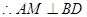 ……1分
……1分
因 ,
,
 满足:
满足: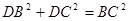 ,
,
所以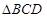 是BC为斜边的直角三角形,
是BC为斜边的直角三角形,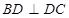 ,
,
因 是
是 的中点,所以ME为
的中点,所以ME为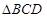 的中位线
的中位线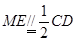 ,
,
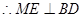 ,
,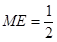 …… 2分
…… 2分
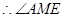 是二面角
是二面角 的平面角
的平面角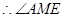 =
= ……3分
……3分
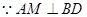 ,
,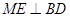 且AM、ME是平面AME内两相交于M的直线
且AM、ME是平面AME内两相交于M的直线
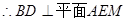
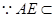 平面AEM
平面AEM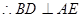 ……4分
……4分
因 ,
,
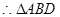 为等腰直角三角形
为等腰直角三角形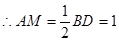 ,
,
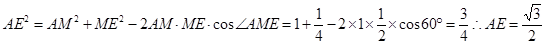
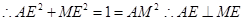 …… 6分
…… 6分
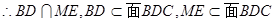
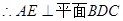 …… 7分
…… 7分
(2)如图,以M为原点MB为x轴,ME为y轴,建立空间直角坐标系,…….. 8分
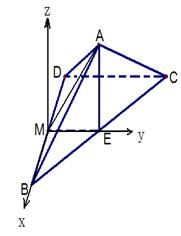 则由(1)及已知条件可知B(1,0,0),
则由(1)及已知条件可知B(1,0,0),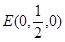 ,
,
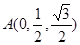 ,D
,D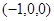 ,C
,C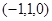
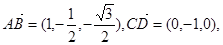 …… 9分
…… 9分
设异面直线 与
与 所成角为
所成角为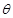 ,
,
则 ……10分
……10分
 ……11分
……11分
由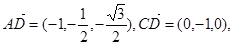 可知
可知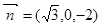 满足,
满足,

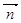 是平面ACD的一个法向量, …… 12分
是平面ACD的一个法向量, …… 12分
记点 到平面
到平面 的距离d,则
的距离d,则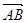 在法向量
在法向量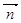 方向上的投影绝对值为d
方向上的投影绝对值为d
则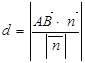 ……13分 所以d
……13分 所以d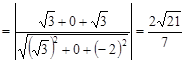 …… 14分
…… 14分
(2),(3)解法二:
取AD中点N,连接MN,则MN是 的中位线,MN//AB,又ME//CD
的中位线,MN//AB,又ME//CD
 所以直线
所以直线 与
与 所成角为
所成角为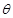 等于MN与ME所成的角,
等于MN与ME所成的角,
即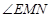 或其补角中较小之一 …… 8分
或其补角中较小之一 …… 8分
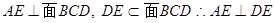 ,N为在
,N为在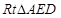 斜边中点
斜边中点
所以有NE=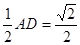 ,MN=
,MN=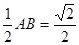 ,ME=
,ME=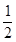 ,
,
 …….9分
…….9分
=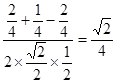 ……10分
……10分
(3)记点 到平面
到平面 的距离d,则三棱锥B-ACD的体积
的距离d,则三棱锥B-ACD的体积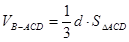 , ……11分
, ……11分
又由(1)知AE是A-BCD的高、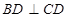
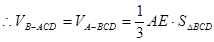 …..12分
…..12分
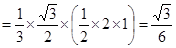
E为BC中点,AE BC
BC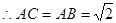 又,
又,
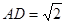 ,
, 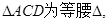
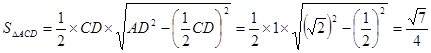 ……13分
……13分
 到平面
到平面 的距离
的距离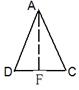
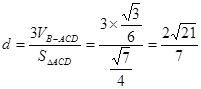 ……14分
……14分
解法三:(1) 因 ,
,
 满足:
满足: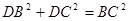 ,
, 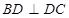 , 1分
, 1分
如图,以D为原点DB为x轴,DC为y轴,建立空间直角坐标系, …….. 2分
则条件可知D(0,0,0), B(2,0,0),C(0,1,0), , A(a,b,c) (由图知a>0,b>0,c>0) …….3分
, A(a,b,c) (由图知a>0,b>0,c>0) …….3分
得
 ….. 4分
….. 4分
平面BCD的法向量可取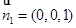 ,
,
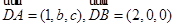 ,所以平面ABD的一个法向量为
,所以平面ABD的一个法向量为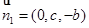 5分
5分
则锐二面角 的余弦值
的余弦值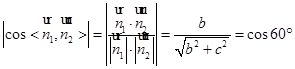 …..6分
…..6分
从而有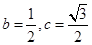 ,
,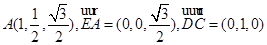 7分
7分
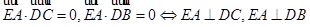 所以
所以 平面
平面 9分
9分
(2)由(1)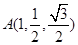 ,D(0,0,0), B(2,0,0),C(0,1,0),
,D(0,0,0), B(2,0,0),C(0,1,0), 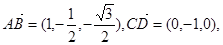
设异面直线 与
与 所成角为
所成角为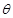 ,则
,则 ……10分
……10分
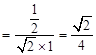 ……11分
……11分
(3)由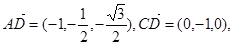 可知
可知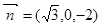 满足,
满足,

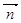 是平面ACD的一个法向量, …… 12分
是平面ACD的一个法向量, …… 12分
记点 到平面
到平面 的距离d,则
的距离d,则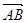 在法向量
在法向量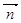 方向上的投影绝对值为d
方向上的投影绝对值为d
则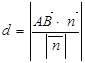 ……13分 所以d
……13分 所以d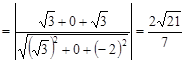 …… 14分
…… 14分
(1)
 如图取BD中点M,连接AM,ME。因
如图取BD中点M,连接AM,ME。因
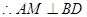 ……1分
……1分因
 ,
,
 满足:
满足: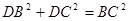 ,
, 所以
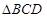 是BC为斜边的直角三角形,
是BC为斜边的直角三角形,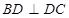 ,
, 因
 是
是 的中点,所以ME为
的中点,所以ME为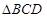 的中位线
的中位线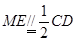 ,
, 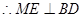 ,
,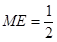 …… 2分
…… 2分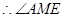 是二面角
是二面角 的平面角
的平面角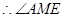 =
= ……3分
……3分 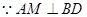 ,
,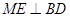 且AM、ME是平面AME内两相交于M的直线
且AM、ME是平面AME内两相交于M的直线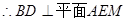
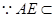 平面AEM
平面AEM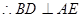 ……4分
……4分因
 ,
,
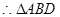 为等腰直角三角形
为等腰直角三角形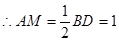 ,
,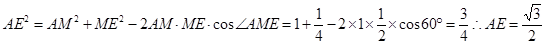
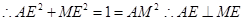 …… 6分
…… 6分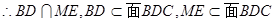
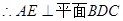 …… 7分
…… 7分(2)如图,以M为原点MB为x轴,ME为y轴,建立空间直角坐标系,…….. 8分
 则由(1)及已知条件可知B(1,0,0),
则由(1)及已知条件可知B(1,0,0),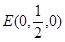 ,
,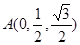 ,D
,D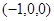 ,C
,C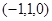
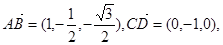 …… 9分
…… 9分设异面直线
 与
与 所成角为
所成角为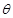 ,
,则
 ……10分
……10分  ……11分
……11分由
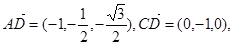 可知
可知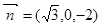 满足,
满足,
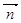 是平面ACD的一个法向量, …… 12分
是平面ACD的一个法向量, …… 12分记点
 到平面
到平面 的距离d,则
的距离d,则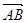 在法向量
在法向量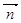 方向上的投影绝对值为d
方向上的投影绝对值为d 则
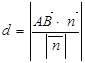 ……13分 所以d
……13分 所以d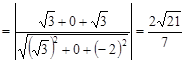 …… 14分
…… 14分(2),(3)解法二:
取AD中点N,连接MN,则MN是
 的中位线,MN//AB,又ME//CD
的中位线,MN//AB,又ME//CD 所以直线
所以直线 与
与 所成角为
所成角为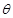 等于MN与ME所成的角,
等于MN与ME所成的角,即
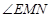 或其补角中较小之一 …… 8分
或其补角中较小之一 …… 8分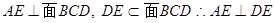 ,N为在
,N为在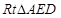 斜边中点
斜边中点所以有NE=
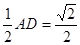 ,MN=
,MN=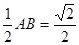 ,ME=
,ME=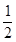 ,
, …….9分
…….9分=
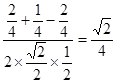 ……10分
……10分(3)记点
 到平面
到平面 的距离d,则三棱锥B-ACD的体积
的距离d,则三棱锥B-ACD的体积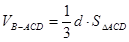 , ……11分
, ……11分又由(1)知AE是A-BCD的高、
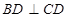
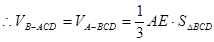 …..12分
…..12分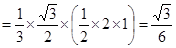
E为BC中点,AE
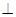 BC
BC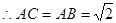 又,
又,
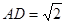 ,
, 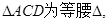
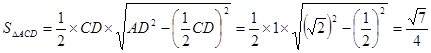 ……13分
……13分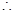
 到平面
到平面 的距离
的距离
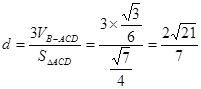 ……14分
……14分 解法三:(1) 因
 ,
,
 满足:
满足: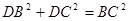 ,
, 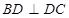 , 1分
, 1分如图,以D为原点DB为x轴,DC为y轴,建立空间直角坐标系, …….. 2分
则条件可知D(0,0,0), B(2,0,0),C(0,1,0),
 , A(a,b,c) (由图知a>0,b>0,c>0) …….3分
, A(a,b,c) (由图知a>0,b>0,c>0) …….3分得

 ….. 4分
….. 4分平面BCD的法向量可取
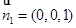 ,
,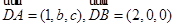 ,所以平面ABD的一个法向量为
,所以平面ABD的一个法向量为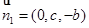 5分
5分则锐二面角
 的余弦值
的余弦值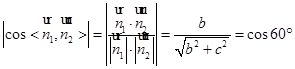 …..6分
…..6分从而有
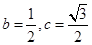 ,
,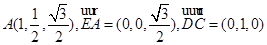 7分
7分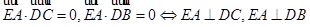 所以
所以 平面
平面 9分
9分(2)由(1)
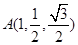 ,D(0,0,0), B(2,0,0),C(0,1,0),
,D(0,0,0), B(2,0,0),C(0,1,0), 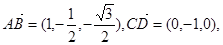
设异面直线
 与
与 所成角为
所成角为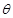 ,则
,则 ……10分
……10分 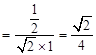 ……11分
……11分(3)由
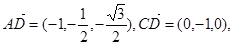 可知
可知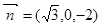 满足,
满足,
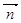 是平面ACD的一个法向量, …… 12分
是平面ACD的一个法向量, …… 12分记点
 到平面
到平面 的距离d,则
的距离d,则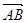 在法向量
在法向量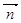 方向上的投影绝对值为d
方向上的投影绝对值为d 则
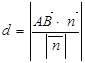 ……13分 所以d
……13分 所以d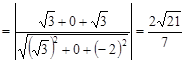 …… 14分
…… 14分略

练习册系列答案
相关题目
 中,
中,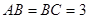 ,
,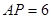 ,
,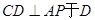 ,现将
,现将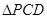 沿线段
沿线段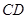 折成
折成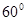 的二面角
的二面角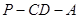 ,设
,设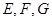 分别是
分别是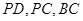 的中点.
的中点.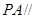 平面
平面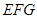 ;
;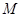 为线段
为线段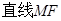 与平面
与平面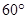 .
.
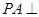 平面ABC,且PA=1,
平面ABC,且PA=1,


 的条件是( )
的条件是( )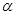 内有无数条直线平行于平面
内有无数条直线平行于平面
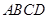 的边长为1,
的边长为1,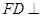 平面
平面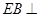 平面
平面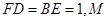 为
为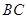 边上的动点。
边上的动点。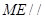 平面
平面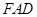 ;
; 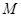 的位置,使平面
的位置,使平面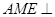 平面
平面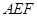 。
。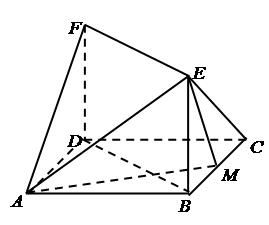




 中,点
中,点 在
在 边上,
边上, ,
, ,
, .
. 的值;
的值; 的面积.
的面积.
 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,
, 是
是 的中点,那么异面直线
的中点,那么异面直线 、
、 所成的角的正切值为 。
所成的角的正切值为 。
 中,
中, ,则
,则 与平面
与平面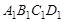 所成的角的大小为: .
所成的角的大小为: .