题目内容
2.在数列{an}中,a1=0,an+1($\frac{5}{2}$-an)=1,令bn=$\frac{{2a}_{n}-1}{{a}_{n}-2}$,且T=b1+2b2+3b3+…+2014b2014,求证:T<$\frac{8}{9}$.分析 通过an+1($\frac{5}{2}$-an)=1、化简可知bn+1=$\frac{2{a}_{n+1}-1}{{a}_{n+1}-2}$=$\frac{1}{4}$•bn,进而可知数列{bn}是以$\frac{1}{2}$为首项、公比为$\frac{1}{4}$的等比数列,利用错位相减法计算即得结论.
解答 证明:∵an+1($\frac{5}{2}$-an)=1,
∴an+1=$\frac{1}{\frac{5}{2}-{a}_{n}}$,
∴bn+1=$\frac{2{a}_{n+1}-1}{{a}_{n+1}-2}$=$\frac{\frac{2}{\frac{5}{2}-{a}_{n}}-1}{\frac{1}{\frac{5}{2}-{a}_{n}}-2}$=$\frac{\frac{4}{5-2{a}_{n}}-1}{\frac{2}{5-2{a}_{n}}-2}$=$\frac{2{a}_{n}-1}{4({a}_{n}-2)}$=$\frac{1}{4}$•bn,
又∵b1=$\frac{2{a}_{1}-1}{{a}_{1}-2}$=$\frac{0-1}{0-2}$=$\frac{1}{2}$,
∴数列{bn}是以$\frac{1}{2}$为首项、公比为$\frac{1}{4}$的等比数列,
∴bn=$\frac{1}{2}$•$\frac{1}{{4}^{n-1}}$=$\frac{2}{{4}^{n}}$,
∴T=b1+2b2+3b3+…+2014b2014=2(1•$\frac{1}{4}$+2•$\frac{1}{{4}^{2}}$+3•$\frac{1}{{4}^{3}}$+…+2014•$\frac{1}{{4}^{2014}}$),
$\frac{1}{4}$T=2(1•$\frac{1}{{4}^{2}}$+2•$\frac{1}{{4}^{3}}$+…+2013•$\frac{1}{{4}^{2014}}$+2014•$\frac{1}{{4}^{2015}}$),
两式相减得:$\frac{3}{4}$T=2($\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{2014}}$-2014•$\frac{1}{{4}^{2015}}$)
=2[$\frac{\frac{1}{4}(1-\frac{1}{{4}^{2014}})}{1-\frac{1}{4}}$-2014•$\frac{1}{{4}^{2015}}$]
=2[$\frac{1}{3}$(1-$\frac{1}{{4}^{2014}}$)-2014•$\frac{1}{{4}^{2015}}$],
∴T=$\frac{4}{3}$•2[$\frac{1}{3}$(1-$\frac{1}{{4}^{2014}}$)-2014•$\frac{1}{{4}^{2015}}$]<$\frac{4}{3}$•2•$\frac{1}{3}$=$\frac{8}{9}$.
点评 本题考查数列的通项及求和,考查运算求解能力,考查错位相减法,注意解题方法的积累,属于中档题.

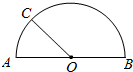 如图,在半径为1的半圆AB,O为圆心,C是半圆周上一点,设弧AC=a,则a>1的概率是$\frac{2}{3}$.
如图,在半径为1的半圆AB,O为圆心,C是半圆周上一点,设弧AC=a,则a>1的概率是$\frac{2}{3}$.