题目内容
用总长14.8米的钢条制作一个长方体容器的框架，如果所制容器底面一边的长比另一边的长多0.5米，那么高为多少时容器的容积最大？最大容积是多少？
x=1时，即h=1.2时，V取到最大值1.8
本试题主要是考查了导数在实际生活中的运用。首先设出变量设底面一边长为x,则另一边长为x+0.5,高为h,容积为V，然后利用体积的公式表示出函数，结合导数的思想来判定单调性，确定出最值。
注意实际问题中，一个极值就是最值。
设底面一边长为x,则另一边长为x+0.5,高为h,容积为V
则4x+4(x+0.5)+4h=14.8,得到 h=3.2-2x
V="x(x+0.5)h" =x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x (0<x<1.6)
由V’=0得x=1或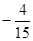
所以，x=1时，即h=1.2时，V取到最大值1.8
注意实际问题中，一个极值就是最值。
设底面一边长为x,则另一边长为x+0.5,高为h,容积为V
则4x+4(x+0.5)+4h=14.8,得到 h=3.2-2x
V="x(x+0.5)h" =x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x (0<x<1.6)
由V’=0得x=1或
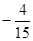
所以，x=1时，即h=1.2时，V取到最大值1.8
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
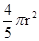分,其中r(单位:cm)是瓶子的半径.已知每出售1ml的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为5cm.
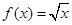的图象在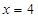
处的切线方程是（ ）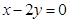
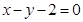
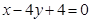
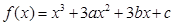在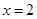
处有极值，其图象在
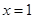处的切线与直线
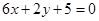平行.
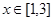时，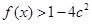
恒成立，求实数
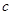的取值范围。
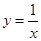在点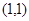
处的切线与直线
垂直，则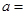
.
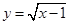相切的切线方程为 （ ）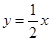
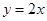
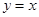
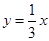
是曲线
上的一点，若曲线在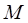
处的切线的倾斜角是均不小于
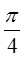的锐角，则实数
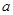的取值范围是（ ）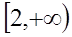
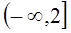
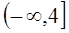
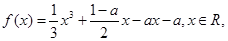其中a>0.