题目内容
(文)已知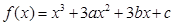 在
在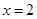 处有极值,其图象在
处有极值,其图象在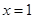 处的切线与直线
处的切线与直线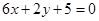 平行.
平行.
(1)求函数的单调区间;
(2)若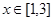 时,
时,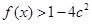 恒成立,求实数
恒成立,求实数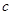 的取值范围。
的取值范围。
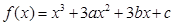 在
在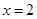 处有极值,其图象在
处有极值,其图象在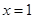 处的切线与直线
处的切线与直线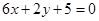 平行.
平行.(1)求函数的单调区间;
(2)若
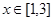 时,
时,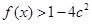 恒成立,求实数
恒成立,求实数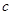 的取值范围。
的取值范围。(1)所以当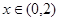 时,函数单调递减;当
时,函数单调递减;当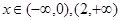 时,函数单调递增。
时,函数单调递增。
(2){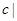
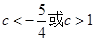 }
}
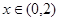 时,函数单调递减;当
时,函数单调递减;当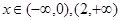 时,函数单调递增。
时,函数单调递增。(2){
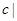
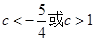 }
} 本试题主要是考查了导数在研究哈数中的运用,以及解决不等式的恒成立的综合运用。
(1)先求解定义域,然后分析导数的符号与单调性的关系,进而得到结论。
(2)根据由(1)知,函数在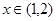 时单调递减,在
时单调递减,在 时单调递增
时单调递增
所以函数在区间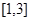 有最小值
有最小值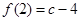 要使
要使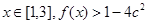 恒成立,可知得到c的不等式解得。
恒成立,可知得到c的不等式解得。
解:(1)由题意: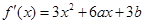 直线
直线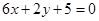 的斜率为
的斜率为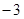 ;
;
由已知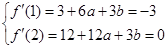 所以
所以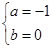 -----------------3分
-----------------3分
所以由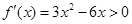 得心
得心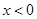 或
或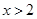 ;
;
所以当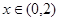 时,函数单调递减;
时,函数单调递减;
当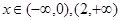 时,函数单调递增。-----------------6分
时,函数单调递增。-----------------6分
(2)由(1)知,函数在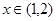 时单调递减,在
时单调递减,在 时单调递增;
时单调递增;
所以函数在区间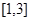 有最小值
有最小值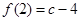 要使
要使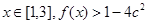 恒成立
恒成立
只需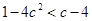 恒成立,所以
恒成立,所以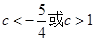 。
。
故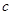 的取值范围是{
的取值范围是{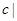
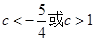 } -----------------10分
} -----------------10分
(1)先求解定义域,然后分析导数的符号与单调性的关系,进而得到结论。
(2)根据由(1)知,函数在
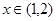 时单调递减,在
时单调递减,在 时单调递增
时单调递增所以函数在区间
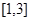 有最小值
有最小值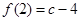 要使
要使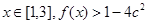 恒成立,可知得到c的不等式解得。
恒成立,可知得到c的不等式解得。解:(1)由题意:
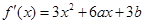 直线
直线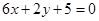 的斜率为
的斜率为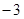 ;
;由已知
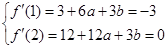 所以
所以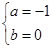 -----------------3分
-----------------3分所以由
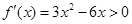 得心
得心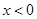 或
或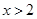 ;
;所以当
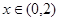 时,函数单调递减;
时,函数单调递减;当
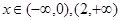 时,函数单调递增。-----------------6分
时,函数单调递增。-----------------6分(2)由(1)知,函数在
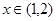 时单调递减,在
时单调递减,在 时单调递增;
时单调递增;所以函数在区间
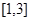 有最小值
有最小值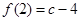 要使
要使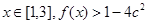 恒成立
恒成立只需
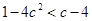 恒成立,所以
恒成立,所以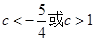 。
。故
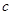 的取值范围是{
的取值范围是{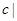
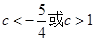 } -----------------10分
} -----------------10分
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
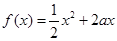 ,
,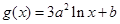 ,其中
,其中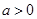 .设两曲线
.设两曲线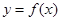 ,
,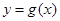 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.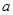 表示
表示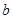 ,并求
,并求 时,
时,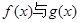 的大小,并证明.
的大小,并证明.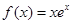 .
.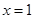 处的切线方程.
处的切线方程.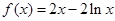
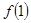 )的切线方程
)的切线方程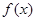 的极值
的极值 ,如果存在曲线上的点
,如果存在曲线上的点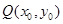 ,且
,且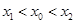 ,使得曲线在点
,使得曲线在点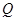 处的切线
处的切线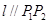 ,则称
,则称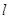 为弦
为弦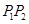 的陪伴切线.
的陪伴切线.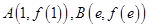 ,试求弦
,试求弦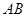 的陪伴切线
的陪伴切线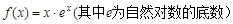
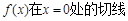 方程;
方程;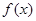 的单调区间.
的单调区间.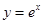 在点
在点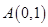 处的切线斜率为
处的切线斜率为 
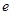
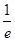

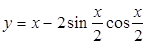 ,则
,则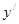 =
= 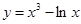 在点(1,2)处的切线方程为
在点(1,2)处的切线方程为