题目内容
10.已知函数p(x)=lnx+1,q(x)=ex,若q(x1)=p(x2)成立,则x2-x1的最小值为1.分析 根据函数图象得出a>0,y=a,a=lnx2+1,x2=ea-1,a=e${\;}^{{x}_{1}}$,x1=lna,构造函数g(a)=ea-1-lna,a>0,利用导数判断单调性,求解最小值即可.
解答 解:∵根据图形得出:a>0,y=a,a=lnx2+1,x2=ea-1,a=e${\;}^{{x}_{1}}$,x1=lna,
∴x2-x1=g(a)=ea-1-lna,a>0,
∵g′(a)=ea-1$-\frac{1}{a}$在(0,+∞)单调递增,
g(1)=0,g(x)>0,x>1;g(x)<0,x<1,
∴g(x)在(1,+∞)单调递增,在(-∞,1)单调递减,
g(x)的最小值为g(1)=e1-1-ln1=1,
∴x2-x1的最小值为1,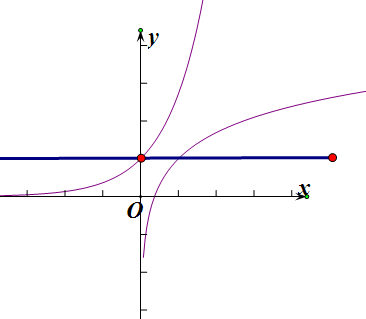
故答案为:1
点评 本题考查了函数的图象的运用,数形结合的思想,构造函数,利用函数的思想求解最近距离问题,考查了学生解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若$\frac{a}{1-i}$=$\frac{1+i}{i}$(i为虚数单位),则a的值为( )
| A. | i | B. | -i | C. | -2i | D. | 2i |
18.已知命题p:“?∈[1,e],a>lnx”,命题q:“?x∈R,x2-4x+a=0””若“p∧q”是真命题,则实数a的取值范围是( )
| A. | (1,4] | B. | (0,1] | C. | [-1,1] | D. | (4,+∞) |
2.已知$\overrightarrow a$,$\overrightarrow b$是平面内夹角为90°的两个单位向量,若向量$\overrightarrow c$满足$(\overrightarrow c-\overrightarrow a)•(\overrightarrow c-\overrightarrow b)=0$,则$|\overrightarrow c|$的最大值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
19.某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽出2听,检测出不合格产品的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
20.已知函数f(x)=cos2x-$\frac{1}{2}$,则( )
| A. | f(x)为偶函数且最小正周期为π | B. | f(x)为奇函数且最小正周期为π | ||
| C. | f(x)为偶函数且最小正周期为2π | D. | f(x)为奇函数且最小正周期为2π |