题目内容
20.若$\frac{a}{1-i}$=$\frac{1+i}{i}$(i为虚数单位),则a的值为( )| A. | i | B. | -i | C. | -2i | D. | 2i |
分析 首先化简复数,利用复数相等的条件得到a.
解答 解:由已知得到$\frac{a(1+i)}{2}=1-i$,设a=x+yi,则(x+yi)(1+i)=2-2i,所以(x-y)+(x+y)i=2-2i,
所以$\left\{\begin{array}{l}{x-y=2}\\{x+y=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$,
所以a=-2i;
故选C.
点评 本题考查了复数的混合运算;关键是注意a,它是复数,容易误认为是实数.

练习册系列答案
相关题目
11.某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据表1
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
${Χ^2}=\frac{{n{{({{n_{11}}{n_{22}}-{n_{12}}{n_{21}}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
| 参加社团活动 | 不参加社团活动 | 合计 | |
| 学习积极性高 | 17 | 8 | 25 |
| 学习积极性一般 | 5 | 20 | 25 |
| 合计 | 22 | 28 | 50 |
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| P(Χ2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(1)抽到参加社团活动的学生的概率是$\frac{11}{25}$,抽到不参加社团活动且学习积极性一般的学生的概率是$\frac{2}{5}$;
(2)有99.9%的把握认为学生的学习积极性与参加社团活动的态度有关系.
8.已知双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
15.已知函数f(x)=xex,则f(x)min=( )
| A. | -1 | B. | -e | C. | -$\frac{1}{e}$ | D. | 不存在 |
5.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
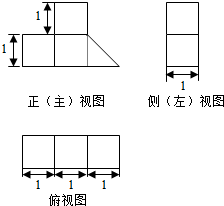

| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |