题目内容
15.若在由正整数构成的无穷数列{an}中,对任意的正整数n,都有an≤an+1,且对任意的正整数k,该数列中恰有2k-1个k,则a2015=45.分析 利用已知条件,推出数列,利用数列的特征求解结果即可.
解答 解:∵对任意的正整数k,该数列中恰有2k-1个k,
∴数列是1;2,2,2;3,3,3,3,3,…
设a2015在第n+1组中,由
1+3+5+…+(2n-1)=n2<2015,解得n<45
∴a2015在第45组中,
所以a2015=45.
故答案为:45.
点评 本题考查数列的递推关系式的应用,数列的函数特征,考查分析问题解决问题的能力.

练习册系列答案
相关题目
5.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
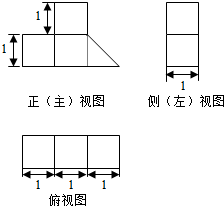

| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
4.已知函数y=f(x)的定义域是[0,2],那么g(x)=$\frac{f({x}^{2})}{1+lg(x+1)}$的定义域是( )
| A. | (-$\frac{9}{10}$,$\sqrt{2}$)∪(-1,-$\frac{9}{10}$) | B. | (-1,$\sqrt{2}$] | C. | (-1,-$\frac{9}{10}$) | D. | (-$\frac{9}{10}$,$\sqrt{2}$) |
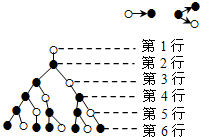 分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照
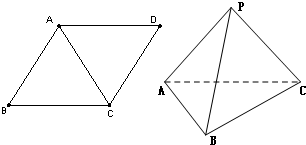
分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照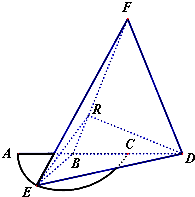 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.