题目内容
18．已知命题p：“?∈[1，e]，a＞lnx”，命题q：“?x∈R，x2-4x+a=0””若“p∧q”是真命题，则实数a的取值范围是（ ）| A． | （1，4] | B． | （0，1] | C． | [-1，1] | D． | （4，+∞） |
分析 先求出命题p，q成立的等价条件，利用命题“p∧q”为真命题，确定实数a的取值范围
解答 解：若命题p：“?∈[1，e]，a＞lnx，为真命题，
则a＞lne=1，
若命题q：“?x∈R，x2-4x+a=0”为真命题，
则△=16-4a≥0，解得a≤4，
若命题“p∧q”为真命题，
则p，q都是真命题，
则$\left\{\begin{array}{l}{a＞1}\\{a≤4}\end{array}\right.$，
解得：1＜a≤4．
故实数a的取值范围为（1，4]．
故选：A．
点评 本题主要考查复合命题与简单命题之间的关系，利用条件先求出命题p，q的等价条件是解决本题的关键．
练习册系列答案
相关题目
8．已知双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点与顶点，若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形，则椭圆的离心率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{1}{2}$ |
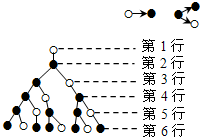分形几何学是美籍法国数学家伯努瓦•曼德尔布罗（BenoitBMandelbrot）在20世纪70年代创立的一门新学科，它的创立为解决传统科学众多领域的难题提供了全新的思路．按照