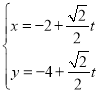Question

【题目】如图，在平面直角坐标系中，已知椭圆的右焦点为，下顶点为P，过点的动直线l交椭圆C于A，B两点.

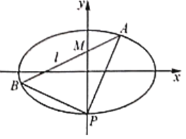
（1）当直线l平行于x轴时，P，F，A三点共线，且，求椭圆C的方程；

（2）当椭圆C的离心率为何值时，对任意的动直线l，总有？

Answer 1

【答案】（1）（2）椭圆C的离心率为

【解析】

（1）当直线与x轴平行，由，得到点坐标，根据，得到的值，将点代入椭圆方程，得到和，从而得到所求椭圆方程；

（2）①当直线l平行于x轴时，由，得到，从而得到，根据得到，从而得到离心率，②当直线l不平行于x轴时，当，椭圆方程转化为，将直线l：与椭圆联立，得到，，再对进行化简，可得，从而得到所求椭圆离心率为.

解：（1）当直线与x轴平行时，即，

如图，作轴于点D，

则根据，可得，

且，

解得，

又因为在椭圆上，所以，

解得

所以，

所以椭圆C的方程为；

（2）①当直线l平行于x轴时，

由，得

∴，又，

∴，∴，

∵，.

②当直线l不平行于x轴时，下面证明当，总有，

事实上，由①知椭圆可化为，

∴，

直线l的方程为，，，

由，得，

∴，

∵，

∴

.

∴，

综上，当椭圆C的离心率为时，对任意的动直线l，总有.