题目内容
【题目】在如图所示的几何体中,D是AC的中点,EF∥DB.
(1)已知AB=BC,AE=EC,求证:AC⊥FB;
(2)已知G,H分别是EC和FB的中点,求证:GH∥平面ABC.
【答案】
(1)
证明:如图所示,
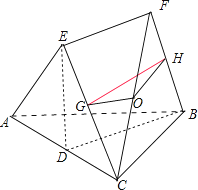
∵D是AC的中点,AB=BC,AE=EC,∴△BAC、△EAC都是等腰三角形,
∴BD⊥AC,ED⊥AC.
∵EF∥DB,∴E、F、B、D四点共面,这样,AC垂直于平面EFBD内的两条相交直线ED、BD,
∴AC⊥平面EFBD.
显然,FB平面EFBD,∴AC⊥FB
(2)
解:已知G,H分别是EC和FB的中点,再取CF的中点O,则OG∥EF,∵OG∥BD,
∴OG∥BD,而BD平面ABC,∴OG∥平面ABC.
同理,OH∥BC,而BC平面ABC,∴OH∥平面ABC.
∵OG∩OH=O,∴平面OGH∥平面ABC,∴GH∥平面ABC.
【解析】(1)由条件利用等腰三角形的性质,证得BD⊥AC,ED⊥AC,再利用直线和平面垂直的判定定理证得AC⊥平面EFBD,从而证得AC⊥FB.(2)再取CF的中点O,利用直线和平面平行的判定定理证明 OG∥平面ABC,OH∥平面ABC,可得平面OGH∥平面ABC,从而证得GH∥平面ABC.;本题主要考查直线和平面垂直的判定和性质,直线和平面平行的判定与性质,属于中档题.

【题目】某校计划面向高一年级1200名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了180名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有105人.在这180名学生中选择社会科学类的男生、女生均为45人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


