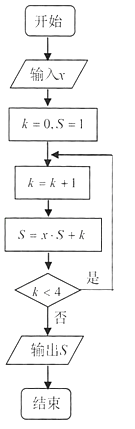
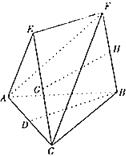
��Ŀ����
����Ŀ��ijУ�ƻ������һ�꼶1200��ѧ������У��ѡ�γ̣�Ϊȷ��������˳��ʵʩ���Ȱ��Ա���зֲ��������ȡ��180��ѧ��������ѧ�࣬��Ȼ��ѧ����������У��ѡ�γ̽���ѡ��������飬����������105�ˣ�����180��ѧ����ѡ������ѧ���������Ů����Ϊ45�ˣ�
���ֱ�����ȡ��������������Ů��ѡ������ѧ���Ƶ�ʣ�����ͳ�Ƶ�Ƶ����Ϊ���ʣ�����ʵ��ѡ����ѡ������ѧ��ѧ������
�����ݳ�ȡ��180��ѧ���ĵ�������������������������ж��ܷ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�����ѡ�����Ա��йأ�
ѡ����Ȼ��ѧ�� | ѡ������ѧ�� | �ϼ� | |
���� | |||
�� | |||
�ϼ� |
���� ![]() ������n=a+b+c+d��
������n=a+b+c+d��
P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡��⣺����������֪����ȡ������Ϊ105�ˣ�Ů��Ϊ180��105=75�ˣ�
����ѡ������ѧ���Ƶ��Ϊ ![]() ��Ů��ѡ������ѧ���Ƶ��Ϊ
��Ů��ѡ������ѧ���Ƶ��Ϊ ![]() ��
��
�����⣬��������Ϊ ![]() �ˣ�
�ˣ�
Ů������Ϊ ![]() �ˣ�
�ˣ�
���ԣ�����ѡ������ѧ������Ϊ ![]() �ˣ�
�ˣ�
������ͳ�����ݣ��ɵ����������£�
ѡ����Ȼ��ѧ�� | ѡ������ѧ�� | �ϼ� | |
���� | 60 | 45 | 105 |
�� | 30 | 45 | 75 |
�ϼ� | 90 | 90 | 180 |
����۲�ֵ ![]() ��
��
���ԣ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�����ѡ�����Ա��йأ�
���������������ȡ��������Ů�����������ݷֲ����ԭ�������Ӧ������Ů��������������ͳ�����ݣ���д������������۲�ֵ���Ƚ��ٽ�ֵ�ó����ۣ�

 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�����Ŀ��ij�ֲ�Ʒ�Ĺ���֧��x�����۶�y����λ����Ԫ��֮�������¶�Ӧ���ݣ�
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
��1����ع�ֱ�߷��̣�
��2����Ԥ�����֧��Ϊ10��Ԫʱ�����۶���
��3�������е����������������ȡ���飬��������һ��������Ԥ��ֵ��ʵ��ֵ֮��ľ���ֵ������5�ĸ��ʣ�