题目内容
【题目】已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
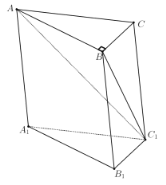
(1)求![]() 的长;
的长;
(2)求![]() 与面
与面![]() 所成的角的正切值.
所成的角的正切值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)方法一:由![]() ,
,![]() ,推出
,推出![]() 面
面![]() ,故
,故![]() ,则可利用勾股定理解出
,则可利用勾股定理解出![]() ;方法一:如图所示以
;方法一:如图所示以![]() 为原点,以
为原点,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,竖直向上为
轴,竖直向上为![]() 轴,建立空间直角坐标系,因为
轴,建立空间直角坐标系,因为![]() 面
面![]() ,即
,即![]() 平面等同于
平面等同于![]() 平面,因而可以利用坐标求出
平面,因而可以利用坐标求出![]() ;
;
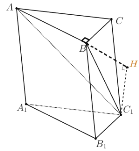
(2)方法一:延长![]() ,过
,过![]() 作
作![]() 于
于![]() ,因为
,因为![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ,所以
,所以![]() 面
面![]() ,所以
,所以![]() 为
为![]() 与面
与面![]() 所成角,等价于
所成角,等价于![]() 与面
与面![]() 所成的角,最后结合数据解三角形即可;方法二:建系后可以利用向量法求出
所成的角,最后结合数据解三角形即可;方法二:建系后可以利用向量法求出![]() 与面
与面![]() 所成的角的正切值.
所成的角的正切值.
解:方法一:(1)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 面
面![]() ,
,
故![]() ,所以
,所以![]() ,
,
于是![]() ;
;
(2)延长![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
由(1)知![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ,
,
又面![]() 面
面![]() ,
,![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
,
所以![]() 为
为![]() 与面
与面![]() 所成角,
所成角,
在![]() 中可得
中可得![]() ,故
,故![]() ,
,![]() ,
,
所以![]() ,
,
又因为![]() ,面
,面![]() 面
面![]() ,
,
故![]() 与面
与面![]() 所成的角即为
所成的角即为![]() 与面
与面![]() 所成的角,
所成的角,
所以![]() 与面
与面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.
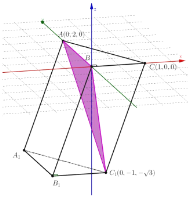
方法二:(1)如图所示以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,竖直向上为
轴,竖直向上为![]() 轴,
轴,
建立空间直角坐标系,则![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 面
面![]() ,即
,即![]() 平面等同于
平面等同于![]() 平面,
平面,
又因为![]() ,
,![]() ,
,
所以![]() 的坐标为
的坐标为![]() ,
,
所以![]() ;
;
(2)因为![]() ,面
,面![]() 面
面![]() ,
,
故![]() 与面
与面![]() 所成的角即
所成的角即![]() 与面
与面![]() 所成的角,设其夹角为
所成的角,设其夹角为![]() ,
,
易得面![]() 的法向量为
的法向量为![]() ,且
,且![]() ,
,
所以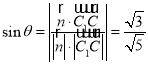 ,
,
所以![]() ,
,
所以![]() 与面
与面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.

练习册系列答案
相关题目
【题目】下表给出的是某城市![]() 年至
年至![]() 年,人均存款
年,人均存款![]() (万元),人均消费
(万元),人均消费![]() (万元)的几组对照数据.
(万元)的几组对照数据.
年份 |
|
|
|
|
人均存款 |
|
|
|
|
人均消费 |
|
|
|
|
(1)试建立![]() 关于
关于![]() 的线性回归方程;如果该城市
的线性回归方程;如果该城市![]() 年的人均存款为
年的人均存款为![]() 万元,请根据线性回归方程预测
万元,请根据线性回归方程预测![]() 年该城市的人均消费;
年该城市的人均消费;
(2)计算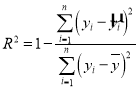 ,并说明线性回归方程的拟合效果.
,并说明线性回归方程的拟合效果.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为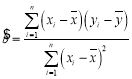 ,
,![]() .
.