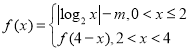题目内容
【题目】已知函数
（
，
为自然对数的底数，
）.
（1）讨论函数
的单调性；
（2）当
时，求使得
恒成立的最小整数
.
【答案】（1）见解析（2）2.
【解析】
（1）对函数进行求导，根据
的不同取值，求出函数的单调性；
（2）结合（1）求出当
时，
的最大值，再根据题意，列出不等式，最后求出的最小整数值.
（1）
，
令
.
当
时，
，所以函数是实数集上的减函数；
当
时，当
，在
上单调递减；当
在
上单调递增；
当
时，当
在
上单调递减；当
在
上单调递增；
（2）由（1）知：当时，函数在时，单调递减，由题意可知：
，得
舍去；
当时，在
上单调递减，由题意可知：，得舍去；
当时，在上单调递增；在
上单调递减，所以有：
，
，可得
，
令
，
由
，可得
，即
，
在
上是单调递增函数，因为
，所以当时，使得
恒成立的最小整数值为2.
练习册系列答案
相关题目
【题目】某高校健康社团为调查本校大学生每周运动的时长，随机选取了80名学生，调查他们每周运动的总时长（单位：小时），按照
共6组进行统计，得到男生、女生每周运动的时长的统计如下（表1、2），规定每周运动15小时以上（含15小时）的称为“运动合格者”，其中每周运动25小时以上（含25小时）的称为“运动达人”.
表1：男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2：女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
（1）从每周运动时长不小于20小时的男生中随机选取2人，求选到“运动达人”的概率；
（2）根据题目条件，完成下面
列联表，并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式：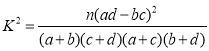
，其中
.
参考数据：
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |
