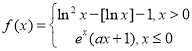题目内容
【题目】已知函数f(x)=|2x-1|+|x+m|.
(l)当m=l时,解不等式f(x)≥3;
(2)证明:对任意x∈R,2f(x)≥|m+1|-|m|.
【答案】(1){x|x≤-1或x≥1};(2)见解析
【解析】
(1)根据绝对值定义将不等式化为三个不等式组,分别求解,最后求并集,(2)根据绝对值三角不等式放缩论证.
(1)当m=1时,f(x)=|2x-1|+|x+1|,
①当x≤-1时,f(x)=-3x≥3,解得x≤-1,
②当-1<x<![]() 时,f(x)=-x+2≥3,解得x≤-1,与-1<x<
时,f(x)=-x+2≥3,解得x≤-1,与-1<x<![]() 矛盾,舍去,
矛盾,舍去,
③当x≥![]() 时,f(x)=3x≥3,解得x≥1,
时,f(x)=3x≥3,解得x≥1,
综上,不等式f(x)<3的解集为{x|x≤-1或x≥1};
(2)2f(x)=|4x-2|+|2x+2m|=|2x-1|+|2x-1|+|2x+2m|≥|2x-1|+|2x+2m|≥|2x+2m-2x+1|
=|2m+1|=|(m+1)+m|≥|m+1|-|m|,
∴对任意x∈R,2f(x)≥|m+1|-|m|.

练习册系列答案
相关题目