题目内容
19.若关于x的方程2ax2-x+2a-1=0的两根均为正实数,则实数a的取值范围是( )| A. | (0,$\frac{1}{2}$) | B. | (-∞,0)∪($\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,$\frac{\sqrt{2}+1}{4}$] |
分析 根据一元二次方程根的个数与△的关系,结合韦达定理,可得关于x的方程2ax2-x+2a-1=0的两根均为正实数时,$\left\{\begin{array}{l}a≠0\\△=1-8a(2a-1)≥0\\ \frac{1}{2a}>0\\ \frac{2a-1}{2a}>0\end{array}\right.$,解得实数a的取值范围.
解答 解:若关于x的方程2ax2-x+2a-1=0的两根均为正实数,
则$\left\{\begin{array}{l}a≠0\\△=1-8a(2a-1)≥0\\ \frac{1}{2a}>0\\ \frac{2a-1}{2a}>0\end{array}\right.$,
解得:a∈($\frac{1}{2}$,$\frac{\sqrt{2}+1}{4}$],
故选:D
点评 本题考查的知识点是一元二次方程根的分布与系数的关系,难度不大,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
7.为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚,为更加详细闯红灯人数的作用,在某一个路口进行了五天试验,得到当天的处罚金额与当天闯红灯人数
(1)根据以上数据,建立当天闯红灯人数y关于当天处罚金额x的回归直线方程;
(2)根据统计数据,上述路口每天经过的行人约为400人,每人闯红灯的可能性相同,在行0元处罚的情况下,记甲、乙、丙三人中闯红灯的人数为X,求X的分布列和数学期望相互独立).
附:回归直线方程中系数计算公式b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}$,$\overline{a}$=$\overline{y}$-b$\overline{x}$.
| 当天处罚金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 当天闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
(2)根据统计数据,上述路口每天经过的行人约为400人,每人闯红灯的可能性相同,在行0元处罚的情况下,记甲、乙、丙三人中闯红灯的人数为X,求X的分布列和数学期望相互独立).
附:回归直线方程中系数计算公式b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}$,$\overline{a}$=$\overline{y}$-b$\overline{x}$.
11.函数f(x)=|ax2+bx+c|(a≠0)的定义域分成四个单调区间的充要条件是 ( )
| A. | a>0且b2-4ac>0 | B. | -$\frac{b}{2a}$>0 | C. | b2-4ac>0 | D. | -$\frac{b}{2a}<0$ |
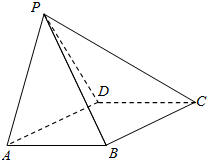 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.