题目内容
1.已知f(x)=log2x,g(x)=lgx.(1)当x为何值时,f(x)=g(x)?
(2)当x为何值时,f(x)>1?
(3)当x为何值时,0<g(x)<1?
分析 (1)利用换底公式将log2x=lgx化简为1-lg2)lgx=0,解决问题.
(2)(3)利用对数函数的单调性即可解出答案.
解答 解:(1)若f(x)=g(x),即log2x=lgx
∴$\frac{lgx}{lg2}$=lgx,
化简得 (1-lg2)lgx=0,
∵1-lg2≠0,∴lgx=0,即x=1.
(2)若log2x>1,即log2x>log22,∴x>2.
(3)若0<lgx<1,即lg1<lgx<lg10,∴1<x<10.
点评 本题考查对数函数的单调性应用,属于基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
11.下列函数中,既是奇函数又在[0,1]上单调递增的是( )
| A. | y=|x|•x3 | B. | y=xlnx | C. | y=x•cosx | D. | $y=-x-\frac{1}{x}$ |
16.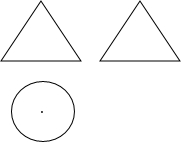 图中的三视图表示的几何体为( )
图中的三视图表示的几何体为( )
 图中的三视图表示的几何体为( )
图中的三视图表示的几何体为( )| A. | 圆柱 | B. | 圆锥 | C. | 圆台 | D. | 三棱柱 |
11.函数f(x)=|ax2+bx+c|(a≠0)的定义域分成四个单调区间的充要条件是 ( )
| A. | a>0且b2-4ac>0 | B. | -$\frac{b}{2a}$>0 | C. | b2-4ac>0 | D. | -$\frac{b}{2a}<0$ |
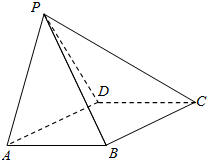 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.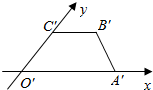 如图是一梯形OABC的直观图.其直观图面积为S,求梯形OABC的面积.
如图是一梯形OABC的直观图.其直观图面积为S,求梯形OABC的面积.