题目内容
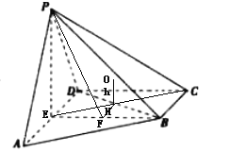
【题目】已知四棱锥![]() 中,底面ABCD是梯形,且
中,底面ABCD是梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,AD的中点为E,则四棱锥
,AD的中点为E,则四棱锥![]() 外接球的表面积为________.
外接球的表面积为________.
【答案】![]()
【解析】
由已知得,![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,那么DEBC是正方形,由
,那么DEBC是正方形,由![]() 平面
平面![]() ,可知
,可知![]() 平面
平面![]() ,可解得PB,可知
,可解得PB,可知![]() 是等边三角形,
是等边三角形,![]() 外接球的球心
外接球的球心![]() 到
到![]() 四点距离相等,设
四点距离相等,设![]() 在平面
在平面![]() 的投影为
的投影为![]() ,根据勾股定理可知点H是对角线的交点,在
,根据勾股定理可知点H是对角线的交点,在![]() 中可得
中可得![]() ,过
,过![]() 作
作![]() 于
于![]() ,再根据
,再根据![]() ,可求出
,可求出![]() ,由外接球面积公式即得。
,由外接球面积公式即得。
由题得,![]() ,
,![]() ,又
,又![]() ,
,![]() 四边形
四边形![]() 是正方形,
是正方形,![]() ,
,![]() 平面
平面![]() ,又
,又![]()
![]() ,
,![]()
![]() 平面
平面![]() ,所以
,所以![]() .则有
.则有![]() ,即
,即![]() ,解得
,解得![]() .
.![]() 球心
球心![]() 到
到![]() 四点距离相等,设
四点距离相等,设![]() 在平面
在平面![]() 的投影为
的投影为![]() ,那么
,那么![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() ,则有
,则有![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]()
![]() ,
,![]()
![]() .
.![]()
![]() 是正方形,
是正方形,![]() 平面
平面![]() 上且到
上且到![]() 四点距离相等的点即为正方形
四点距离相等的点即为正方形![]() 的对称中心,即对角线的交点,则
的对称中心,即对角线的交点,则![]() .
.![]()
![]() .过
.过![]() 作
作![]() 于
于![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() ,
,![]()
![]() 平面
平面![]() ,即
,即![]() 是点
是点![]() 在平面
在平面![]() 的投影.
的投影.![]()
![]() 是等边三角形,
是等边三角形,![]()
![]() ,
,![]() ,
,![]()
![]() ,与
,与![]() 联立解得
联立解得![]() ,则
,则![]() .
.
故答案为:![]()

 名校课堂系列答案
名校课堂系列答案【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率作了调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如表:
个人所得税税率表 | 个人所得税税率表 | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率 | 级数 | 全月应纳税所得额 | 税率 |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
|
|
|
|
|
|
(1)假如小明某月的工资、薪金等税前收入为7500元,请你帮小明算一下调整后小明的实际收入比调整前增加了多少?
(2)某税务部门在小明所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入 |
|
|
|
|
|
|
人数 | 40 | 30 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量X表示抽到作为宣讲员的收入在
的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量X表示抽到作为宣讲员的收入在![]() 元的人数,求X的分布列与数学期望.
元的人数,求X的分布列与数学期望.
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的![]() 班和文史类专业的
班和文史类专业的![]() 班各抽取
班各抽取![]() 名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
优秀 | 非优秀 | 总计 | |
| 14 | 6 | 20 |
| 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
附:参考公式及数据:
(1)统计量:![]() ,(
,(![]() ).
).
(2)独立性检验的临界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
则下列说法正确的是
A. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
B. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关
C. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
D. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关