题目内容
2.考察下列各式
你能做出什么一般性的猜想?能证明你的猜想吗?
分析 直接利用已知条件,猜想写出结果,然后利用数学归纳法证明即可.
解答 解:猜想:(n+1)(n+2)(n+3)…2n=2n×1×3×5…(2n-1).
证明:(1)当n=1时,显然成立.
(2)假设当n=k时等式成立,即(k+1)(k+2)(k+3)…2k=2k×1×3×5…(2k-1).
那么当n=k+1时(k+1+1)(k+1+2)(k+1+3)…2(k+1)
=$(k+1)\frac{(k+1+1)(k+1+2)(k+1+3)•…•2k(2k+1)2(k+1)}{k+1}$
=$\frac{{2}^{k}×1×3×5•…•(2k-1)(2k+1)2(k+1)}{k+1}$
=2k+1×1×3×5×…×[2(k+1)-1],
所以当n=k+1时等式成立.
根据(1)(2)可知对任意正整数等式均成立.
点评 本题考查归纳推理,数学归纳法的证明步骤的应用,考查计算能力,逻辑推理能力.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
12.sin33°•sin63°+cos63°•sin57°的值等于( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.在正方体ABCD-A1B1C1D1中,B1C与对角面DD1B1B所成角的大小是( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
11.表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x吨与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图.
(2)根据上表数据用最小二乘法求出y关于x的线性回归方程.
(3)由(2)预测技改后生产100吨甲产品的生产能耗是多少吨标准煤?(参考数值:3*2.5+4*3+5*4+6*4.5=66.5)
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)根据上表数据用最小二乘法求出y关于x的线性回归方程.
(3)由(2)预测技改后生产100吨甲产品的生产能耗是多少吨标准煤?(参考数值:3*2.5+4*3+5*4+6*4.5=66.5)
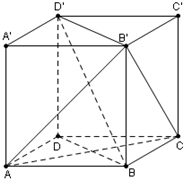 正方体ABCD-A′B′C′D′中,求证:
正方体ABCD-A′B′C′D′中,求证: