题目内容
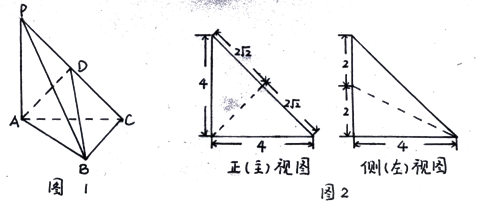
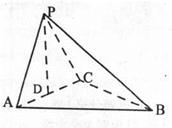
(本小题13分)如图1,在三棱锥P—ABC中,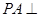 平面ABC,
平面ABC,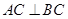 ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
(1)证明: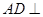 平面PBC;
平面PBC;
(2)求三棱锥D—ABC的体积;
(3)在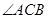 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得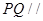 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。
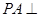 平面ABC,
平面ABC,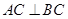 ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
(1)证明:
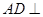 平面PBC;
平面PBC;(2)求三棱锥D—ABC的体积;
(3)在
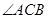 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得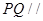 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。(1)根据已知题意,可知 ,然后结合
,然后结合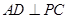 来得到证明。
来得到证明。
(2)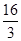 (3)
(3)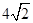
 ,然后结合
,然后结合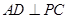 来得到证明。
来得到证明。(2)
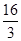 (3)
(3)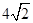
试题分析:(1)由主视图可知D为PC中点,
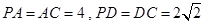
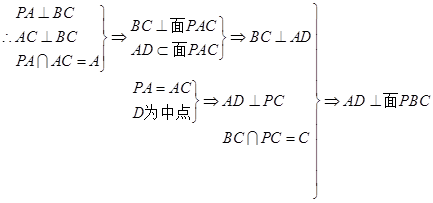
(2)
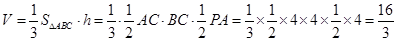
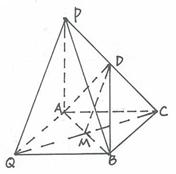
(3)设
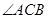 的角平分线交AB于M,连DM,CM并延长CM至
的角平分线交AB于M,连DM,CM并延长CM至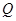 ,使得
,使得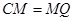 ,连接
,连接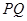
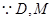 分别是
分别是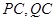 的中点,
的中点,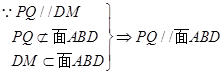
又
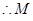 为AB、CQ中点
为AB、CQ中点 ∴四边形ACBQ为正方形
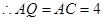
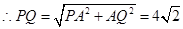
点评:解决的关键是对于线面垂直的判定定理和性质定理的运用,属于基础题。

练习册系列答案
相关题目
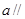 平面
平面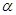 ,则
,则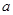 平行;
平行;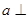 平面
平面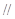 平面
平面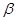 ,则
,则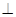 平面
平面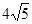
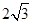 ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值. 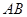 、
、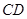 在原正方体的位置关系是( )
在原正方体的位置关系是( )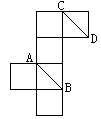
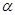 、
、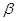 .下列四个命题中,
.下列四个命题中,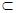
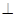
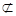
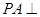 ⊙
⊙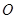 所在的平面,AB是⊙
所在的平面,AB是⊙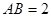 ,
,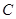 是⊙
是⊙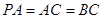 ,
,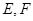 分别为
分别为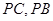 中点。
中点。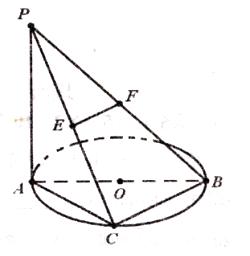
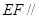 平面
平面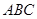 ;
;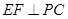 ;
;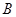 -
-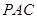 的体积。
的体积。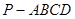 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱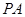 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点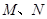 分别是
分别是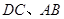 的中点.求
的中点.求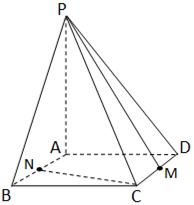
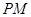 与
与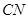 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);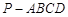 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,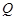 是棱
是棱 上的动点.
上的动点.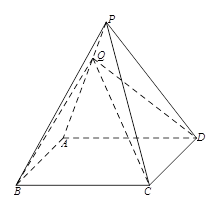
 是
是 //平面
//平面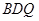 ;
;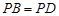 ,求证:
,求证: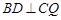 ;
;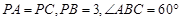 ,求四棱锥
,求四棱锥