题目内容
(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
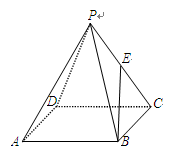
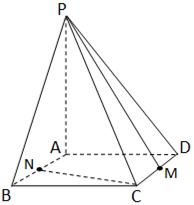
如图已知四棱锥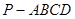 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱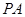 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点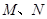 分别是
分别是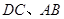 的中点.求
的中点.求
(1)异面直线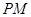 与
与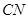 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)四棱锥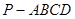 的表面积.
的表面积.
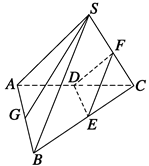
如图已知四棱锥
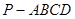 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱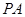 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点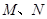 分别是
分别是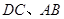 的中点.求
的中点.求
(1)异面直线
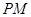 与
与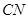 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);(2)四棱锥
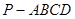 的表面积.
的表面积. (1)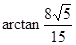 .(2) 144
.(2) 144
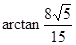 .(2) 144
.(2) 144试题分析:
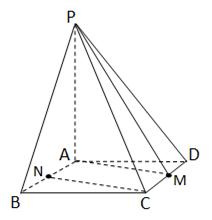
(1)解法 一:连结
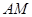 ,可证
,可证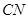 ∥
∥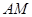 ,直线
,直线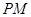 与
与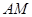 所成角等于直线
所成角等于直线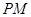 与
与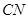 所成角.因为
所成角.因为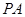 垂直于底面,所以
垂直于底面,所以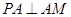 ,点
,点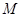 分别是
分别是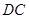 的中点,
的中点, 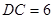
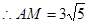 ,在
,在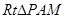 中,
中,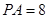 ,
,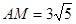 ,
,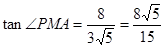 ,
,
即异面直线
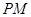 与
与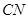 所成角的大小为
所成角的大小为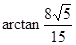 .
. 解法二:以
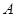 为坐标原点建立空间直角坐标系可得
为坐标原点建立空间直角坐标系可得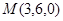 ,
,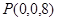 ,
,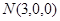 ,
,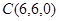 ,
,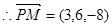 ,
,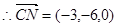
直线
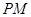 与
与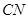 所成角为
所成角为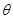 ,向量
,向量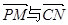 的夹角为
的夹角为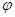
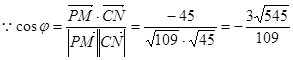
又
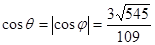 ,
,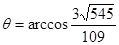 ,
,即异面直线
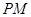 与
与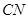 所成角的大小为
所成角的大小为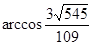 .
.(说明:两种方法难度相当)
(2) 因为
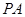 垂直于底面,所以
垂直于底面,所以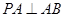 ,
,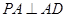 即
即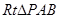 ≌
≌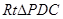
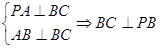 ,同理
,同理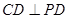
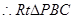 ≌
≌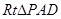 …………8分
…………8分底面四边形
 是边长为6的正方形,所以
是边长为6的正方形,所以
又
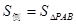
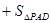
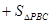
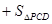

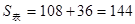
所以四棱锥
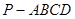 的表面积是144
的表面积是144点评:高考中的立体几何问题主要是探求和证明空间几何体中的平行和垂直关系以及空间角、体积等计算问题.对于平行和垂直问题的证明或探求,其关键是把线线、线面、面面之间的关系进行灵活的转化.在寻找解题思路时,不妨采用分析法,从要求证的结论逐步逆推到已知条件

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
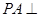 平面ABC,
平面ABC,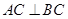 ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。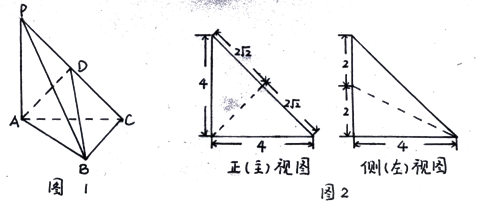
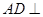 平面PBC;
平面PBC;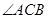 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得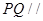 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD,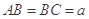 ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且

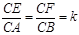 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 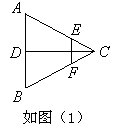
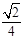 ,求k的值.
,求k的值. 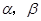 截球O的两个截面圆的半径分别为1和
截球O的两个截面圆的半径分别为1和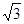 .若二面角
.若二面角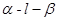 的平面角为150°,则球O的表面积为
的平面角为150°,则球O的表面积为



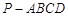 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )