题目内容
13.在矩形ABCD中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AD}$|=2,则|$\overrightarrow{BA}+\overrightarrow{BD}+\overrightarrow{BC}$|=( )| A. | 12 | B. | 6 | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |
分析 由已知得到所求是对角线BD长度的2倍,只要求出矩形的对角线即可.
解答 解:由已知矩形ABCD中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AD}$|=2,则|$\overrightarrow{BA}+\overrightarrow{BD}+\overrightarrow{BC}$|=|$\overrightarrow{BD}+\overrightarrow{BD}$|=2|$\overrightarrow{BD}$|=2$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{20}$=4$\sqrt{5}$;
故选C.
点评 本题考查了向量的平行四边形法则的运用以及向量模的求法;解答本题的关键是明确所求为矩形的对角线长度的计算.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.从2010名学生中选50人组成参观团,先用简单随机抽样方法剔除10人,再将其余2000人从0到1999编号,按等距系统抽样方法选取,若第一组采用抽签法抽到的号码是30,则最后一组入选的号码是( )
| A. | 1990 | B. | 1991 | C. | 1989 | D. | 1988 |
1.函数f(x)=lnx-$\frac{1}{2}{x^2}$的单调递增区间为( )
| A. | (-∞,-1)与(1,+∞) | B. | (0,1)∪(1,+∞) | C. | (0,1) | D. | (1,+∞) |
8.随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下2×2列联表:
(1)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为“性别与是否读营养说明之间有关系”?
(2)若采用分层抽样的方法从读营养说明的学生中随机抽取3人,则男生和女生抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求恰有一男一女的概率.
| 读营养说明 | 不读营养说明 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 12 | 20 |
| 合计 | 24 | 16 | 40 |
(2)若采用分层抽样的方法从读营养说明的学生中随机抽取3人,则男生和女生抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求恰有一男一女的概率.
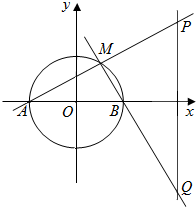 在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.
在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.