题目内容
6.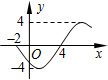 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
分析 根据三角函数的图象确定A,ω和φ的值即可得到结论.
解答 解:由图象知A=4,T=2[4-(-2)]=12,
则T=$\frac{2π}{ω}$=12,即ω=$\frac{π}{6}$,
则f(x)=4sin($\frac{π}{6}$x+φ),
由五点对应法得$\frac{π}{6}$×4+φ=0,
即φ=-$\frac{2π}{3}$,
故f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$),
故答案为:f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
点评 本题主要考查三角函数解析式的求解,根据三角函数图象确定A,ω和φ的值是解决本题的关键.

练习册系列答案
相关题目
17.在△ABC中,若sinA:sinB:sinC=2:3:4,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 不能确定 |
11.在下列四个函数中,在区间(0,$\frac{π}{2}$)上为增函数,且以π为最小正周期的偶函数是( )
| A. | y=tanx | B. | y=|sinx| | C. | y=sin2x | D. | y=cos2x |
15.已知向量$\vec a,\vec b$满足|$\vec a$|=2,|$\vec b$=3,|2$\vec a$+$\vec b$|=$\sqrt{37}$,则向量$\vec a$与$\vec b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
16.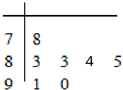 在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
 在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85和6.8 | B. | 85和1.6 | C. | 86和6.8 | D. | 86和1.6 |