在数列{an}中.已知a1=2.an+1=$\frac{2{a} {n}}{{a} {n+1}}$.求论证{$\frac{1}{{a} {n}}$-1}是等比数列.并求数列{an}的通项公式．题目和参考答案——青夏教育精英家教网——

题目内容

14．在数列{a_n}中，已知a₁=2，a_n+1=

\frac{2 a_{n}}{a_{n + 1}}

$\frac{2{a}_{n}}{{a}_{n+1}}$ ，求论证{

\frac{1}{a_{n}}

$\frac{1}{{a}_{n}}$ -1}是等比数列，并求数列{a_n}的通项公式．

分析根据递推关系是求解得出 $\frac{1}{{a}_{n+1}}$ -1= $\frac{1}{2}$ [ $\frac{1}{{a}_{n}}$ -1]，运用等比数列定义 $\frac{\frac{1}{{a}_{n+1}}-1}{\frac{1}{{a}_{n}}-1}$ = $\frac{1}{2}$ =常数．可判断求解．

解答解：∵a_n+1= $\frac{2{a}_{n}}{{a}_{n+1}}$ ，a₁=2，
∴ $\frac{1}{{a}_{n+1}}$ -1= $\frac{1}{2}$ [ $\frac{1}{{a}_{n}}$ -1]， $\frac{1}{{a}_{1}}$ = $\frac{1}{2}-1$ = $-\frac{1}{2}$ ，
∴ $\frac{\frac{1}{{a}_{n+1}}-1}{\frac{1}{{a}_{n}}-1}$ = $\frac{1}{2}$ =常数．
{ $\frac{1}{{a}_{n}}$ -1}是以 $-\frac{1}{2}$ 为首项，以 $\frac{1}{2}$ 为公比的等比数列，
∴ $\frac{1}{{a}_{n}}$ -1=（ $-\frac{1}{2}$ ）×（ $\frac{1}{2}$ ）^n-1=-（ $\frac{1}{2}$ ）ⁿ，
∴ $\frac{1}{{a}_{n}}$ =1- $\frac{1}{{2}^{n}}$
即a_n= $\frac{{2}^{n}}{{2}^{n}-1}$

点评本题利用数列的递推关系是求解转化为等比数列求解通项公式，属于容易题，关键是恒等变形得出需要的条件．

练习册系列答案

小升初名师帮你总复习系列答案

成长阅读系列答案

小学毕业升学考试总复习系列答案

赢在阅读限时提优训练系列答案

同步解析拓展训练系列答案

星火英语SPARK系列答案

单元检测新疆电子音像出版社系列答案

新课标数学口算天天练系列答案

恒基中考备战策略系列答案

七星图书口算速算天天练系列答案

相关题目

4．在等差数列{a_n}中，a₁=2，a₄=5，则a₇=8．

5．已知△ABC中，角A、B、C成等差数列，求证：

\frac{1}{a + b}

$\frac{1}{a+b}$ +

\frac{1}{b + c}

$\frac{1}{b+c}$ =

\frac{3}{a + b + c}

$\frac{3}{a+b+c}$ ．

2．当x＞2时，不等式x+

\frac{1}{x - 2}

$\frac{1}{x-2}$ ≥a恒成立，则实数a的最大值是4．

9．下列命题中，不正确的是（　　）

$|\overrightarrow a|=\sqrt{{{（\overrightarrow a）}^2}}$

$\overrightarrow a$ •

$\overrightarrow b$ ）=

$\overrightarrow a$ •（λ

$\overrightarrow b$ ）

$\overrightarrow a$ -

$\overrightarrow b$ ）

$\overrightarrow c$ =

$\overrightarrow a$ •

$\overrightarrow c$ -

$\overrightarrow b$ •

$\overrightarrow c$

$\overrightarrow a$ 与

$\overrightarrow b$ 共线?

$\overrightarrow a$ •

$\overrightarrow b$ =

$|{\overrightarrow a}||{\overrightarrow b}|$

19．若复数z=i（2-z），则z=1+i．

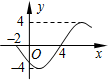函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则该函数的解析式为f（x）=4sin（

$\frac{π}{6}$ x-

$\frac{2π}{3}$ ）．

3．设函数f（x）=sin（2x+

$\frac{π}{3}$ ）+2sinxcosx．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若x∈[-

$\frac{π}{12}$ ，

$\frac{π}{3}$ ]，求函数f（x）的最大值和最小值．

4．直角坐标系内的一动点，运动时该点坐标满足不等式y＞x，则这个动点的运动区域（用阴影表示）是（　　）