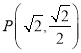题目内容
【题目】(1)直线![]() 在矩阵
在矩阵![]() 所对应的变换
所对应的变换![]() 下得到直线
下得到直线![]() ,求
,求![]() 的方程.
的方程.
(2)已知点![]() 是曲线
是曲线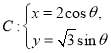 (
(![]() 为参数,
为参数,![]() )上一点,
)上一点,![]() 为坐标原点直线
为坐标原点直线![]() 的倾斜角为
的倾斜角为![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)求不等式![]() 的解集.
的解集.
【答案】(1)![]() ;(2)
;(2)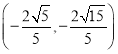 ;(3)
;(3)![]()
【解析】
(1)先在直线![]() 上取点
上取点![]() ,
,![]() 在矩阵
在矩阵![]() 的变换下得到
的变换下得到![]() ,再在直线
,再在直线![]() 上取点
上取点![]() ,在矩阵
,在矩阵![]() 的变换下得到
的变换下得到![]() ,进而可求出
,进而可求出![]() 的方程;
的方程;
(2)根据曲线的参数方程,得到普通方程,根据题意得到直线的直角坐标方程,两式联立,即可求出结果;
(3)分![]() ,
,![]() ,
,![]() 三种情况讨论,分别求解,即可求出结果.
三种情况讨论,分别求解,即可求出结果.
(1)解:在直线![]() 上取点
上取点![]() ,
,
![]() ,故
,故![]() 在矩阵
在矩阵![]() 的变换下得到
的变换下得到![]() ,
,
再在直线![]() 上取点
上取点![]() ,
,
![]() ,在矩阵
,在矩阵![]() 的变换下得到
的变换下得到![]() ,
,
连接![]() ,可得直线
,可得直线![]() .
.
(2)解:由题意得,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
联立方程组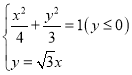 ,解得
,解得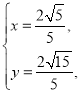 (舍去),或
(舍去),或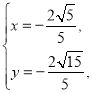
故点![]() 的直角坐标为
的直角坐标为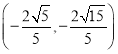 .
.
(3)解:①当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
②当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
③当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上,原不等式的解集为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目