题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
【答案】(1)![]() ; (2)①见解析;②见解析.
; (2)①见解析;②见解析.
【解析】
(1)根据离心率、焦距和![]() 可解出
可解出![]() ,从而得到椭圆方程;(2)①设直线
,从而得到椭圆方程;(2)①设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() ,将直线方程与椭圆方程联立可得韦达定理的形式,从而求得
,将直线方程与椭圆方程联立可得韦达定理的形式,从而求得![]() ;整理可知:
;整理可知:![]() ,从而证得结论;②
,从而证得结论;②![]() 与
与![]() 关于
关于![]() 轴对称可知
轴对称可知![]() ,由①知
,由①知![]() ,则
,则![]() ,利用两角和差正切公式展开整理,根据基本不等式求得最小值,经验证等号无法取得,从而证得结论.
,利用两角和差正切公式展开整理,根据基本不等式求得最小值,经验证等号无法取得,从而证得结论.
(1)由题意可得: ,解得:
,解得:
![]()
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]()
(2)证明:①设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]()
由 消去
消去![]() 得:
得:![]()
则![]() ,且
,且![]() ,
,![]()
![]()

即直线![]() 的斜率依次成等比数列
的斜率依次成等比数列
②由题可知:![]()
由①可知:![]() ,
,![]() ,
,![]()
![]()
![]()
若![]() ,则
,则![]() 两点重合,不符合题意;可知无法取得等号
两点重合,不符合题意;可知无法取得等号
![]()

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)求![]() 与
与![]() 的相关系数
的相关系数![]() 精确到0.01,并判断
精确到0.01,并判断![]() 与
与![]() 的关系是否可用线性回归方程模型拟合?(规定:
的关系是否可用线性回归方程模型拟合?(规定:![]() 时,可用线性回归方程模型拟合);
时,可用线性回归方程模型拟合);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型
,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:(1)相关系数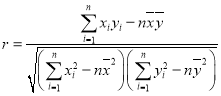
(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
