题目内容
2．在数列2，$\frac{5}{2}$，3，$\frac{7}{2}$，4…中，第21项为12．分析 根据数列项的规律求出数列的通项公式即可．
解答 解：数列等价为$\frac{4}{2}$，$\frac{5}{2}$，$\frac{6}{2}$，$\frac{7}{2}$，$\frac{8}{2}$…中，
则对应的通项公式为an=$\frac{n+3}{2}$，
则第21项为a21=$\frac{21+3}{2}=\frac{24}{2}$=12，
故答案为：12．
点评 本题主要考查数列的概念和简单表示，求出数列的规律是解决本题的关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
12．
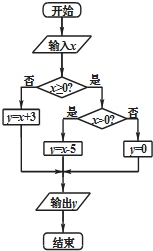执行如图所示的程序框图，在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入，则输出的y值落在区间[-4，3]内的概率为（ ）
执行如图所示的程序框图，在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入，则输出的y值落在区间[-4，3]内的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{6}$ |
17．过正四棱锥（侧棱长全是1，侧面三角形的顶角为30度）的底面一个顶点的平面截棱锥所得四边形的周长的最小值是（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
7．对于函数f（x），若满足f（x0）=x0，则称x0为f（x）的不动点．现有函数g（x）=ex+x2-t（t∈R），记h（x）=g（g（x）），若存在m∈[0，1]为h（x）的不动点，则t的取值范围是（ ）
| A． | [0，1] | B． | [1，e] | C． | [1，1+e] | D． | [e，e+1] |