题目内容
17.过正四棱锥(侧棱长全是1,侧面三角形的顶角为30度)的底面一个顶点的平面截棱锥所得四边形的周长的最小值是( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 把正四棱锥的四个侧面以顶点为公共点展开,容易得出截棱锥所得四边形的周长的最小值是什么.
解答 解:如图所示,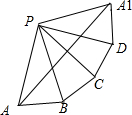
把正四棱锥P-ABCD的四个侧面以顶点为公共点展开,
连接AA1,则AA1是截棱锥所得四边形的周长的最小值;
又PA=PA1,∠APA1=4×30°=120°,
∴${{AA}_{1}}^{2}$=PA2+${{PA}_{1}}^{2}$-2PA•PA1•cos120°
=12+12-2×1×1×(-$\frac{1}{2}$)
=3,
∴AA1=$\sqrt{3}$;
即截棱锥所得四边形的周长最小值是$\sqrt{3}$.
故选:D.
点评 本题考查了空间几何体的平面展开图的应用问题,也考查了转化思想的应用问题,是基础题目.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
7.已知f(x)=x2+3xf′(1),则f′(1)为( )
| A. | -1 | B. | -2 | C. | 0 | D. | 1 |
8.若$tan\frac{α}{2}=2$,则tanα等于( )
| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -3 | D. | $\frac{3}{4}$ |
6.将两枚质地均匀的骰子各掷一次,设事件A={两个点数互不相同},B={出现一个5点},则P(B|A)=( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
7.用反证证明:“自然数a,b,c中恰有一个偶数”时正确的假设为( )
| A. | a,b,c都是偶数 | B. | a,b,c都是奇数 | ||
| C. | a,b,c中至少有两个偶数 | D. | a,b,c中都是奇数或至少两个偶数 |
 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),给出以下说法:
已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),给出以下说法: