题目内容
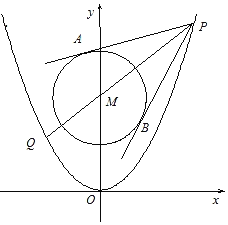
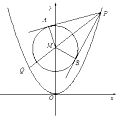
【题目】已知抛物线C1:x2=2py(p>0),圆C2:x2+y2﹣8y+12=0的圆心M到抛物线C1的准线的距离为![]() ,点P是抛物线C1上一点,过点P,M的直线交抛物线C1于另一点Q,且|PM|=2|MQ|,过点P作圆C2的两条切线,切点为A、B.
,点P是抛物线C1上一点,过点P,M的直线交抛物线C1于另一点Q,且|PM|=2|MQ|,过点P作圆C2的两条切线,切点为A、B.
(Ⅰ)求抛物线C1的方程;
(Ⅱ)求直线PQ的方程及![]()
![]()
![]() 的值.
的值.
【答案】(Ⅰ)x2=2y;(Ⅱ)21
【解析】
(Ⅰ)由已知条件推导出4![]() ,由此能求出抛物线C1的方程.
,由此能求出抛物线C1的方程.
(Ⅱ)设PQ的方程:y=kx+4,由![]() ,得x2﹣2kx﹣8=0,由此利用韦达定理结合已知条件能求出直线PQ的方程及
,得x2﹣2kx﹣8=0,由此利用韦达定理结合已知条件能求出直线PQ的方程及![]()
![]()
![]() 的值.
的值.
(Ⅰ)![]() ,∴M(0,4),
,∴M(0,4),
抛物线![]() 的准线方程是y
的准线方程是y![]() ,
,
依题意:4![]() ,∴p=1,
,∴p=1,
∴抛物线C1的方程为:x2=2y.
(Ⅱ)设PQ的方程:y=kx+4,
由![]() ,得x2﹣2kx﹣8=0,设P(x1,y1),Q(x2,y2),
,得x2﹣2kx﹣8=0,设P(x1,y1),Q(x2,y2),
则![]() ,
,
∵|PM|=2|MQ|,∴![]() ,∴﹣x1=2x2,①
,∴﹣x1=2x2,①
又x1+x2=2k,…②,x1x2=﹣8,③,
由①②③得k=±1,
∴PQ的方程为:y=±x+4.
取PQ的方程:y=x+4,和抛物线x2=2y,联立得P点坐标为P(4,8)
∴|![]() |=4
|=4![]() ,连接AM,BM,|
,连接AM,BM,|![]() |=|
|=|![]() |
|![]() ,
,
设∠APM=α,则sinα![]() ,
,
∴![]() |
|![]() |
|![]() |
|![]() |cos2α
|cos2α
=28(1﹣2sin2α)=21.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目