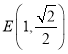题目内容
【题目】已知抛物线![]() 和
和![]() 轴上的定点
轴上的定点![]() ,过抛物线焦点作一条直线交
,过抛物线焦点作一条直线交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() 并延长,交
并延长,交![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求证:直线![]() 过定点;
过定点;
(2)求直线![]() 与直线
与直线![]() 最大夹角为
最大夹角为![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)当直线![]() 、
、![]() 斜率不存在时,可直接求解;当直线
斜率不存在时,可直接求解;当直线![]() 、
、![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,联立方程组得
,联立方程组得![]() ,
,![]() ,
, ,
, ,结合
,结合![]() 可得直线
可得直线![]() ,即可得证;
,即可得证;
(2)当直线![]() 斜率存在时,易证
斜率存在时,易证![]() ,利用
,利用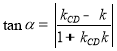 求出最大值即可得解.
求出最大值即可得解.
(1)证明:由题意知抛物线焦点![]() ,
,
当直线![]() 斜率不存在时,直线
斜率不存在时,直线![]() ,易得
,易得![]() ,
,![]() ,
,
则直线![]() ,
,![]() ,
,
所以点![]() ,
,![]() ,此时直线
,此时直线![]() ;
;
当线![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,
,
则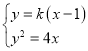 ,化简得
,化简得![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
①当![]() 时,则
时,则![]() ,所以
,所以![]() ,
,![]() ,点
,点![]() ,
,
所以直线![]() ,点
,点![]() ,
,
直线![]() ,则
,则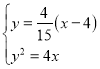 解得点
解得点![]() ,
,
所以直线![]() ;
;
②当![]() 时,此时直线
时,此时直线![]() ,
,
则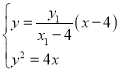 ,结合
,结合![]() 化简得
化简得![]() ,
,
此方程有一根为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以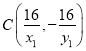 ,
,
同理可得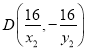 ,
,
由![]() ,
,![]() ,
,![]() 可得
可得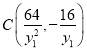 ,
,![]() ,
,
所以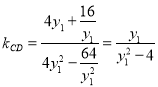 ,
,
所以直线![]() ,化简得
,化简得![]() ,
,
可得直线![]() 过点
过点![]() ;
;
综上,直线![]() 恒过点
恒过点![]() ;
;
(2)由(1)知,当直线![]() 斜率不存在时,
斜率不存在时,![]() ;
;
当直线斜率![]() 存在时,
存在时,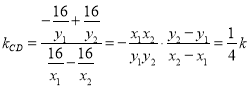 ,
,
设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,
,
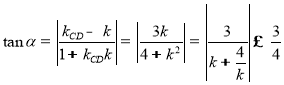 ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
所以对于直线![]() 与直线
与直线![]() 最大夹角
最大夹角![]() ,
,![]() .
.

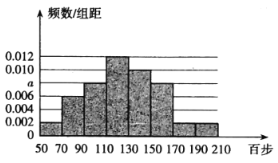
【题目】某学校为进一步规范校园管理,强化饮食安全,提出了“远离外卖,健康饮食”的口号.当然,也需要学校食堂能提供安全丰富的菜品来满足同学们的需求.在学期末,校学生会为了调研学生对本校食堂A部和B部的用餐满意度,从在A部和B部都用过餐的学生中随机抽取了200人,每人分别对其评分,满分为100分.随后整理评分数据,将分数分成6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
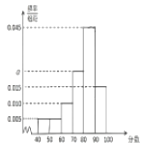
,第6组![]() ,得到A部分数的频率分布直方图和B部分数的频数分布表.
,得到A部分数的频率分布直方图和B部分数的频数分布表.
分数区间 | 频数 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定义:学生对食堂的“满意度指数”
分数 |
|
|
|
|
|
|
满意度指数 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位数(精确到小数点后一位);
(2)A部为进一步改善经营,从打分在80分以下的前四组中,采用分层抽样的方法抽取8人进行座谈,再从这8人中随机抽取3人参与“端午节包粽子”实践活动,在第3组抽到1人的情况下,第4组抽到2人的概率;
(3)如果根据调研结果评选学生放心餐厅,应该评选A部还是B部(将频率视为概率)