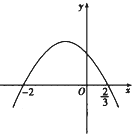
题目内容
【题目】【选修4-4:坐标系与参数方程】
在极坐标系中,已知点![]() 到直线
到直线![]() 的距离为3.
的距离为3.
(1)求实数![]() 的值;
的值;
(2)设![]() 是直线
是直线![]() 上的动点,
上的动点, ![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹方程,并指出轨迹是什么图形.
的轨迹方程,并指出轨迹是什么图形.
【答案】(1)![]() (2)点
(2)点![]() 的轨迹是以
的轨迹是以![]() 为圆心,
为圆心, ![]() 为半径的圆.
为半径的圆.
【解析】试题分析:(1)先根据![]() 将直线极坐标方程化为直角坐标方程
将直线极坐标方程化为直角坐标方程![]() ,再根据点到直线距离公式求实数
,再根据点到直线距离公式求实数![]() 的值;(2)利用转移法求动点轨迹:设
的值;(2)利用转移法求动点轨迹:设![]() ,则可得
,则可得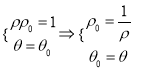 ,再代人对应极坐标方程
,再代人对应极坐标方程![]() ,化简可得点
,化简可得点![]() 的轨迹方程,最后根据
的轨迹方程,最后根据![]() 将极坐标方程化为直角坐标方程,化成标准式,判断轨迹形状.
将极坐标方程化为直角坐标方程,化成标准式,判断轨迹形状.
试题解析:解:(1)以极点为原点,极轴为![]() 轴的正半轴,建立直角坐标系,
轴的正半轴,建立直角坐标系,
则点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
∵点![]() 到直线
到直线![]() 的距离为
的距离为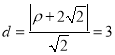 , ∴
, ∴![]() .
.
(2)设![]() ,则
,则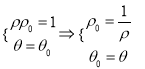 ①
①
∵点![]() 在直线
在直线![]() 上, ∴
上, ∴![]() ②
②
将①代入②,得![]() ,即
,即![]() ,这就是点
,这就是点![]() 的轨迹方程,化为直角坐标方程为
的轨迹方程,化为直角坐标方程为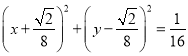 ,因此点
,因此点![]() 的轨迹是以
的轨迹是以![]() 为圆心,
为圆心, ![]() 为半径的圆.
为半径的圆.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目