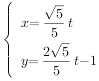题目内容
【题目】已知函数f(x)=3x﹣3ax+b且 ![]() ,
, ![]() .
.
(1)求a,b的值;
(2)判断f(x)的奇偶性,并用定义证明.
【答案】
(1)解:∵函数f(x)=3x﹣3ax+b, ![]() ,
, ![]() ,
,
∴ 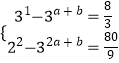 ,即
,即 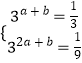 ,即
,即 ![]() ,∴a=﹣1,b=0
,∴a=﹣1,b=0
(2)解:由(1)可得f(x)=3x﹣3﹣x,它的定义域为R,关于原点对称,
再根据f(﹣x)=3﹣x﹣3x=﹣f(3x﹣3﹣x)=﹣f(x),故该函数为奇函数
【解析】(1)由条件利用待定系数法求得a、b的值,可得函数的解析式.(2)根据的定义域为R,关于原点对称,再根据f(﹣x)=﹣f(x),从而得出结论.
【考点精析】关于本题考查的函数的奇偶性和函数的零点,需要了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能得出正确答案.

练习册系列答案
相关题目