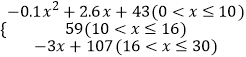题目内容
【题目】定义域为R的函数f(x)= ![]() (x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
(x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
A.0
B.21g2
C.31g2
D.1
【答案】C
【解析】解:当x=2时,f(x)=1,则由f2(x)+bf(x)+c=0得1+b+c=0.∴x1=2,c=﹣b﹣1.
当x>2时,f(x)=lg(x﹣2),由f2(x)+bf(x)+c=0得[lg(x﹣2)]2+blg(x﹣2)﹣b﹣1=0,解得lg(x﹣2)=1,x2=12或lg(x﹣2)=b,x3=2+10b .
当x<2时,f(x)=lg(2﹣x),由f2(x)+bf(x)+c=0得[lg(2﹣x)]2+blg(2﹣x)﹣b﹣1=0),解得lg(2﹣x)=1,x4=﹣8或lg(2﹣x)=b,x5=2﹣10b .
∴f(x1+x2+x3+x4+x5)=f(2+12+2+10b﹣8+2﹣10b)=f(10)=lg|10﹣2|=lg8=3lg2.
故选C.

练习册系列答案
相关题目