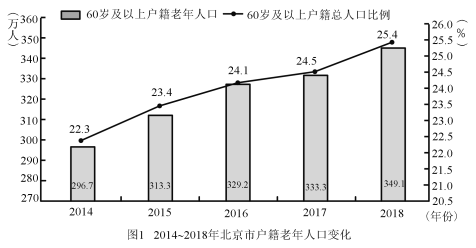
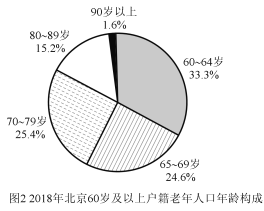
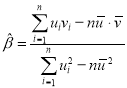题目内容
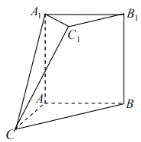
【题目】如图1，四边形ABCD为矩形，BC=2AB，E为AD的中点，将
ABE、DCE分别沿BE、CE折起得图2，使得平面
平面BCE，平面
平面BCE.
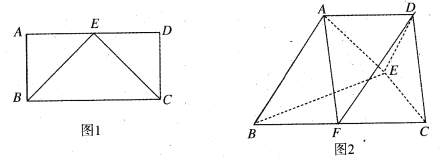
（1）求证：平面平面DCE；
（2）若F为线段BC的中点，求直线FA与平面ADE所成角的正弦值.
【答案】（1）证明见解析；（2）
.
【解析】
（1）证明
平面ABE，平面
平面DCE即得证；
（2）以点E为坐标原点，EB,EC所在的直线分别为
轴，
轴建立空间直角坐标系，设
，利用向量法求直线FA与平面ADE所成角的正弦值得解.
（1）证明：在图1中，BC=2AB，且E为AB的中点，
，同理
.
所以
，
又平面平面BCE，平面
平面
，
所以平面ABE，又
平面
，
所以平面平面DCE.
（2）
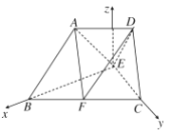
如图，以点E为坐标原点，EB,EC所在的直线分别为轴，轴建立空间直角坐标系，设，
则
.
向量
，设平面ADE的法向量为
由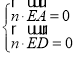
，得
，令
，
得平面ADE的一个法向量为
，
又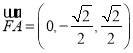
，
设直线FA与平面ADE所成角为
，
则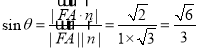
所以直线FA与平面ADE所成角的正弦值为.
名校课堂系列答案
【题目】近年来，政府相关部门引导乡村发展旅游的同时，鼓励农户建设温室大棚种植高品质农作物.为了解某农作物的大棚种植面积对种植管理成本的影响，甲，乙两同学一起收集6家农户的数据，进行回归分折，得到两个回归摸型：模型①：
，模型②： 
，对以上两个回归方程进行残差分析，得到下表：
种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
模型② |
| 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
（1）将以上表格补充完整，并根据残差平方和判断哪个模型拟合效果更好；
（2）视残差
的绝对值超过1.5的数据视为异常数据，针对（1）中拟合效果较好的模型，剔除异常数据后，重新求回归方程.
附：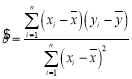
，
；
