Question

【题目】已知数列{an}的前n项和Sn=2an﹣2n+1 ， 若不等式2n2﹣n﹣3＜（5﹣λ）an对n∈N*恒成立，则整数λ的最大值为（　　）
A.3
B.4
C.5
D.6

Answer 1

【答案】B
【解析】解：当n=1时，a1=S1=2a1﹣22 ， 得a1=4；
当n≥2时，Sn﹣1=2an﹣1﹣2n ， 又Sn=2an﹣2n+1 ，
两式相减得，an=2an﹣1+2n ，
即有 ．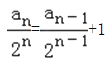
又=2，
则数列{}是以2为首项，1为公差的等差数列，
=2+n﹣1，
即an=（n+1）2n ，
∵an＞0，∴不等式2n2﹣n﹣3＜（5﹣λ）an ， 等价于5﹣λ＞ ．
记bn= ．
n≥2时， ．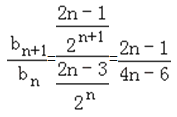
∴n≥3时，＜1，（bn）max=b3= ．
∴5﹣λ＞ ， 即λ＜5﹣= ，
∴整数λ的最大值为4．
故选：B．