题目内容
【题目】已知y＝f(x)是定义在R上的偶函数，当x
0时，f(x)＝
.
(1)求当x<0时，f(x)的解析式；
(2)作出函数f(x)的图象，并指出其单调区间．
【答案】(1) 当x<0时，f(x) 
(2) 递减区间是(－∞，0]，递增区间是[0，＋∞)．
【解析】
试题利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一，给出函数在x>0的解析式，利用当x<0时，-x>0,借助f(x)=f(-x)就可以求出x<0时的解析式；作函数图象最好先观察一下函数的解析式的形式特点，了解一下函数的简单性质，利用图象变换作图象又快又准，
左移2个单位得出
的图象，取
的部分，y轴左边的图象与y轴右边的图象关于y轴对称.根据图象写出单调区间.
试题解析：
(1)当x<0时，－x>0，
∴f(－x)＝
，
又f(x)是定义在R上的偶函数，
∴f(－x)＝f(x)，
∴当x<0时，
.
(2)由(1)知，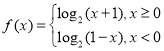
作出f(x)的图象如图所示：
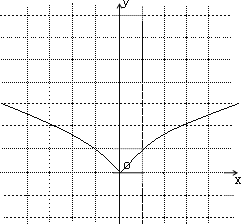
由图得函数f(x)的递减区间是(－∞，0]，递增区间是[0，＋∞)．
天天向上口算本系列答案
【题目】“共享单车”的出现，为我们提供了一种新型的交通方式．某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图如图： 
（Ⅰ）根据茎叶图，比较两城市满意度评分的平均值的大小及方差的大小（不要求计算出具体值，给出结论即可）；
（Ⅱ）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此2×2列联表，并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关；
A | B | 合计 | |
认可 | |||
不认可 | |||
合计 |
（Ⅲ）若从此样本中的A城市和B城市各抽取1人，则在此2人中恰有一人认可的条件下，此人来自B城市的概率是多少？
附：参考数据：
（参考公式： 
）