Question

【题目】已知定义在R上的奇函数f（x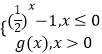）= ，则f（1）=；不等式f（f（x））≤7的解集为 ．

Answer 1

【答案】﹣1；（﹣∞，2]
【解析】解：∵R上的奇函数f（x）= ，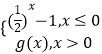
∴f（1）=﹣f（﹣1）=﹣[（ ）﹣1﹣1]=﹣1，
∵不等式f（f（x））≤7，f（﹣3）=7，
∴f（x）≥﹣3，
∵R上的奇函数f（x）= ，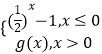
∴g（x）=1﹣2x ，
∴f（x）≥﹣3等价于 或 ，
可以解得x≤2，
即不等式f（f（x））≤7的解集为（﹣∞，2]．
所以答案是：﹣1；（﹣∞，2]．
【考点精析】通过灵活运用函数奇偶性的性质，掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇即可以解答此题．