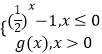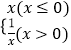题目内容
【题目】已知a为实数,若函数f(x)=|x2+ax+2|﹣x2在区间(﹣∞,﹣1)和(2,+∞)上单调递减,则实数a的取值范围为 .
【答案】[﹣8,0)
【解析】解:f(x)=|x2+ax+2|﹣x2= ![]() ,
,
设x2+ax+2=0的两个根分别为x1 , x2 , (x1<x2),
则f(x)= ![]() ,
,
∵当x≥x2时,函数f(x)=ax+2,函数f(x)在(2,+∞)上单调递减,
∴a<0,
当x1<x<x2时,抛物线的对称轴为x=﹣ ![]() =﹣
=﹣ ![]() .
.
若函数f(x)在(2,+∞)上单调递减,则﹣ ![]() ≤2,得﹣8≤a<0.
≤2,得﹣8≤a<0.
若f(x)在区间(﹣∞,﹣1)递减,
则x1= ![]() ≥﹣1,
≥﹣1,
即﹣a﹣ ![]() ≥﹣2,
≥﹣2,
则 ![]() ≥a﹣2,
≥a﹣2,
∵﹣8≤a<0,
∴ ![]() ≥a﹣2恒成立,
≥a﹣2恒成立,
综上﹣8≤a<0,
所以答案是:[﹣8,0)
【考点精析】掌握函数的单调性是解答本题的根本,需要知道注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.

练习册系列答案
相关题目