题目内容
已知二次函数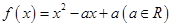 同时满足:
同时满足:
①不等式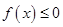 的解集有且只有一个元素;
的解集有且只有一个元素;
②在定义域内存在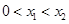 ,使得不等式
,使得不等式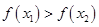 成立.
成立.
数列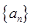 的通项公式为
的通项公式为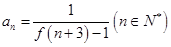 .
.
(1)求函数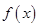 的表达式;
的表达式;
(2)求数列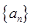 的前
的前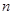 项和
项和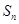 .
.
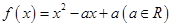 同时满足:
同时满足:①不等式
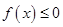 的解集有且只有一个元素;
的解集有且只有一个元素;②在定义域内存在
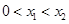 ,使得不等式
,使得不等式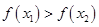 成立.
成立.数列
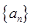 的通项公式为
的通项公式为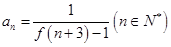 .
.(1)求函数
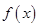 的表达式;
的表达式; (2)求数列
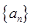 的前
的前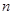 项和
项和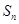 .
.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)首先根据二次函数
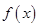 的开口方向以及不等式
的开口方向以及不等式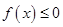 的解集只有一个元素这些条件得到
的解集只有一个元素这些条件得到 ,结合函数
,结合函数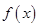 在区间
在区间 上的单调性得出
上的单调性得出 的值,进而求出函数
的值,进而求出函数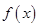 的解析式;(2)先求出数列
的解析式;(2)先求出数列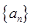 的通项公式
的通项公式 ,利用裂项相消法求数列
,利用裂项相消法求数列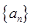 的前
的前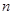 项和
项和 .
.试题解析:(1)
 ,且不等式
,且不等式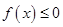 的解集有且只有一个元素,
的解集有且只有一个元素,则
 ,解得
,解得 或
或 ,
,又由于定义域内存在
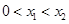 ,有
,有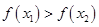 ,则函数
,则函数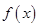 在区间
在区间 上不是增函数,
上不是增函数,因此
 ,所以
,所以 ,
, ;
;(2)
 ,
,所以
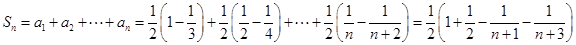
 .
.
练习册系列答案
相关题目
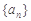 中,
中,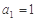 ,
,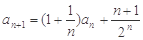 .
.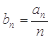 ,求数列
,求数列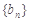 的通项公式;
的通项公式;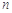 项和
项和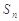 .
. 的前
的前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 满足
满足 ,
, ,
, ;
; 的前
的前 .
.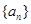 中,
中,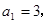 前
前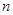 和
和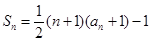
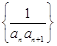 的前
的前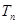 ,是否存在实数
,是否存在实数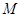 ,使得
,使得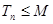 对一切正整数
对一切正整数 的通项
的通项 ,其前n项和为
,其前n项和为 .
.  ;
; 求数列{
求数列{ }的前n项和
}的前n项和 .
.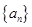 的前n项和
的前n项和 =
= -2n+1,则通项公式
-2n+1,则通项公式 =
=
 的通项公式为
的通项公式为 ,那么满足
,那么满足 的整数
的整数 ( )
( )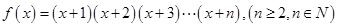 ,其导函数为
,其导函数为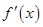 ,设
,设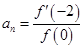 ,则数列
,则数列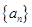 自第2项到第
自第2项到第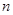 项的和
项的和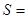 _____________.
_____________. 中,
中, ,
,  ,
,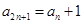 ,则
,则
 = .
= .