题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() 是椭圆
是椭圆![]() 的左右顶点,点
的左右顶点,点![]() 是椭圆
是椭圆![]() 上一动点,
上一动点,![]() 的周长为6,且直线
的周长为6,且直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 、
、![]() 为椭圆
为椭圆![]() 上位于
上位于![]() 轴同侧的两点,且
轴同侧的两点,且![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)根据题意,得到![]() ,
,![]() ,再由
,再由![]() ,求出
,求出![]() ,
,![]() ,即可得出椭圆方程;
,即可得出椭圆方程;
(2)由![]() 得
得![]() ,延长
,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 与椭圆方程,根据韦达定理,弦长公式,以及三角形面积公式,得到四边形
与椭圆方程,根据韦达定理,弦长公式,以及三角形面积公式,得到四边形![]() 的面积
的面积![]() ,令
,令![]() ,
,![]() ,得到
,得到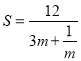 ,进而可得出结果.
,进而可得出结果.
(1)∵![]() 的周长为6,∴
的周长为6,∴![]() ,即
,即![]() ,①
,①
设![]() ,因为点
,因为点![]() ,
,![]() 是椭圆
是椭圆![]() 的左右顶点,则
的左右顶点,则![]() ,
,![]() ,
,
因为直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() ,
,
所以![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ②
②
联立①②及![]() ,解得
,解得![]() ,
,![]() ,
,![]() .
.
∴椭圆![]() 的方程为
的方程为![]() ;
;
(2)∵![]() ,∴
,∴![]() ,
,
延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,
,
由(1)知![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立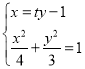 ,得
,得![]() .
.
∴![]() ,
,![]() .
.
由对称性可知,![]() ,设
,设![]() 与
与![]() 的距离为
的距离为![]() ,
,
则四边形![]() 的面积
的面积
![]() .
.
∴![]()
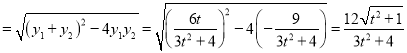 .
.
令![]() ,
,![]() .
.
∴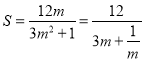 .
.
易知:![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() .
.
故四边形![]() 面积的取值范围为
面积的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目