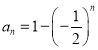题目内容
【题目】意大利人斐波那契在1202年写的《计算之书》中提出一个兔子繁殖问题:假设一对刚出生的小兔一个月后能长成大兔,再过一个月便能生下一对小兔,此后每个月生一对小兔,如此,设第n个月的兔子对数为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….考查数列
,….考查数列![]() 的规律,不难发现,
的规律,不难发现,![]() (
(![]() ),我们称该数列为斐波那契数列.
),我们称该数列为斐波那契数列.
(1)若数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() (
(![]() ,
,![]() ),试判断数列
),试判断数列![]() 是否构成斐波那契数列,说明理由;
是否构成斐波那契数列,说明理由;
(2)若数列![]() 是斐波那契数列,且
是斐波那契数列,且![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)若数列![]() 是斐波那契数列,求数列
是斐波那契数列,求数列![]() 的前n项和
的前n项和![]() .
.
【答案】(1)![]() 是斐波那契数列;详见解析(2)证明见解析(3)
是斐波那契数列;详见解析(2)证明见解析(3)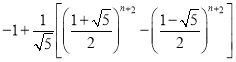
【解析】
(1)利用![]() 证得
证得![]() ,同时计算出
,同时计算出![]() ,证得结论;
,证得结论;
(2)变形![]() 与
与![]() 比较,同时计算出
比较,同时计算出![]() ,得证等比数列;
,得证等比数列;
(3)由(2)得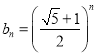 ,即
,即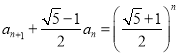 ,此式可变形为
,此式可变形为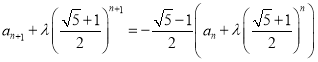 ,化简得
,化简得![]() ,这样由等比数列通项公式得
,这样由等比数列通项公式得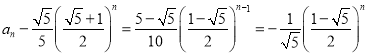 ,从而得
,从而得![]() ,再分组后由等比数列的前
,再分组后由等比数列的前![]() 项和公式可得.
项和公式可得.
解:(1)因为![]() ,
,![]() (
(![]() ,
,![]() ).
).
所以![]() ①,
①,![]() ②
②
②-①得![]() ,又
,又![]() ,故
,故![]() 是斐波那契数列;
是斐波那契数列;
(2)因为![]() ,所以
,所以
![]()

![]()
![]() ,即
,即![]() ,
,
即 ,所以
,所以![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列;
为公比的等比数列;
(3)由(2)得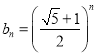 ,即
,即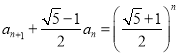 ,
,
令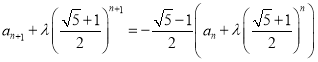 ,化简得
,化简得![]() ,
,
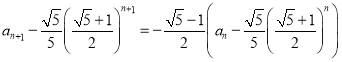
因为![]() ,所以
,所以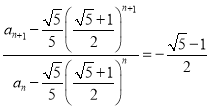
即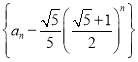 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,故
为公比的等比数列,故
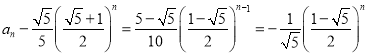
即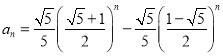 ;
;
所以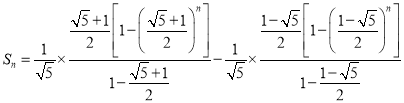
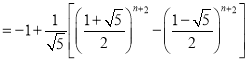 .
.

【题目】现有一款智能学习APP,学习内容包含文章学习和视频学习两类,且这两类学习互不影响,已知该APP积分规则如下:每阅读一篇文章积1分,每日上限积5分;观看视频累计3分钟积2分,每日上限积6分,经过抽样统计发现,文章学习积分的概率分布表如表1所示,视频学习积分的概率分布表如表2所示.
表1
文章学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
【题目】随着互联网金融的不断发展,很多互联网公司推出余额增值服务产品和活期资金管理服务产品,如蚂蚁金服旗下的“余额宝”,腾讯旗下的“财富通”,京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况,随机抽取1200名使用理财产品的市民,按照使用理财产品的情况统计得到如下频数分布表:
分组 | 频数(单位:名) |
使用“余额宝” |
|
使用“财富通” |
|
使用“京东小金库” | 30 |
使用其他理财产品 | 50 |
合计 | 1200 |
已知这1200名市民中,使用“余额宝”的人比使用“财富通”的人多160名.
(1)求频数分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余额宝”的平均年化收益率为![]() ,“财富通”的平均年化收益率为
,“财富通”的平均年化收益率为![]() .若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为
.若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为![]() ,求
,求![]() 的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为
的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为![]() ”即将100元钱存入某理财产品,一年可以获得3元利息.
”即将100元钱存入某理财产品,一年可以获得3元利息.