题目内容
【题目】已知椭圆![]() ,
,![]() 、
、![]() 为椭圆的左、右焦点,
为椭圆的左、右焦点,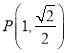 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 、直线
、直线![]() 于
于![]() 、
、![]() 两点,当
两点,当![]() 最小时,求直线
最小时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]() .
.
【解析】
(1)设椭圆的左焦点![]() ,由
,由![]() ,解得
,解得![]() ,再结合椭圆的定义,求得
,再结合椭圆的定义,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)可设直线![]() ,联立方程组,求得
,联立方程组,求得![]() ,利用弦长公式,求得
,利用弦长公式,求得![]() 和
和![]() 的长,进而得到
的长,进而得到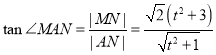 ,利用基本不等式,求得
,利用基本不等式,求得![]() 的值,即可求解.
的值,即可求解.
(1)设椭圆的左焦点![]() ,则
,则![]() ,解得
,解得![]() ,
,
所以![]() ,则由椭圆定义
,则由椭圆定义![]() ,∴
,∴![]() ,
,![]()
故椭圆的标准方程为![]() .
.
(2)由题意直线![]() 的斜率必定不为零,于是可设直线
的斜率必定不为零,于是可设直线![]() ,
,
联立方程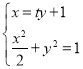 得
得![]() ,
,
∵直线![]() 交椭圆于
交椭圆于![]() ,
,![]() ,
,
∴![]()
由韦达定理![]() ,
,![]()
则![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
又![]()
∴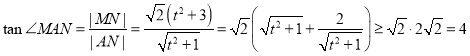
当且仅当![]() 即
即![]() 时取等号.
时取等号.
此时直线![]() 的方程为
的方程为![]() 或
或![]() .
.

【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的650名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: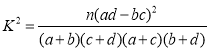 ,其中
,其中![]() .
.
【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
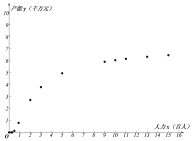
(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为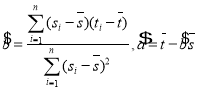 ,(说明:
,(说明:![]() 的导函数为
的导函数为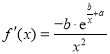 )
)