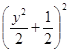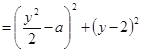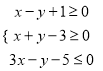Question

【题目】已知，若的任何一条对称轴与轴成交点的横坐标都不属于区间，则的取值范围是（ ）

A. B.

C. D.

Answer 1

【答案】C

【解析】分析：由题意可得， ≥3π﹣2π=π，求得＜ω≤1，故排除A、D．检验当ω=时，f（x）=sin（x﹣）满足条件，故排除B，从而得出结论．

详解：f（x）=sinωx﹣cosωx=sin（ωx﹣）（ω＞，x∈R），

若f（x）的任何一条对称轴与x轴交点的横坐标都不属于区间（2π，3π），

则≥3π﹣2π=π，ω≤1，即＜ω≤1，故排除A、D．

当ω=时，f（x）=sin（x﹣），

令x﹣=kπ+，求得 x=kπ+，可得函数f（x）的图象的对称轴为 x=kπ+，k∈Z．

当k=1时，对称轴为 x=＜2π，当k=2时，对称轴为 x==3π，

满足条件：任何一条对称轴与x轴交点的横坐标都不属于区间（2π，3π），故排除B，

故选：C．