已知实数x.y满足$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ 0≤y≤3\end{array}\right.$.则z=3x-y的取值范围是( )A．[-3.6]B．[-3.12]C．[-6.12]D．[3.6] 题目和参考答案——青夏教育精英家教网—

题目内容

2．已知实数x，y满足$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ 0≤y≤3\end{array}\right.$，则z=3x-y的取值范围是（　　）

A．

[-3，6]

B．

[-3，12]

C．

[-6，12]

D．

[3，6]

分析先画出可行域，再把目标函数变形为直线的斜截式，根据其在y轴上的截距即可求之．

解答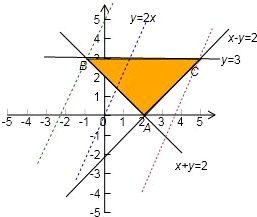解：画出可行域，如图所示
解得B（-1，3）、C（5，3），
把z=3x-y变形为y=3x-z，则直线经过点B时z取得最小值；经过点C时z取得最大值，
所以z_min=3×（-1）-3=-6，z_max=3×5-3=12，
即z的取值范围是[-6，12]．
故选：C．

点评本题考查利用线性规划求函数的最值，是一道基础题．

练习册系列答案

13．设不等式组$\left\{\begin{array}{l}x＞0\\ y＞0\\ y≤-nx+3n\end{array}\right.$所表示的平面区域为D_n，记D_n内的格点（格点即横坐标和纵坐标均为整数的点）个数为f（n）（n∈N^*）
（1）求f（1），f（2）的值及f（n）的表达式；
（2）若数列{a_n}满足a₁=1，${a_{n+1}}-{a_n}=f（n），（n∈{N^•}）$，求数列{a_n}的通项公式；
（3）设S_n为数列{b_n}的前n项的和，其中${b_n}={2^{f（n）}}$，问是否存在正整数n，t，使$\frac{{{S_n}-t{b_n}}}{{{S_{n+1}}-t{b_{n+1}}}}＜\frac{1}{16}$成立？若存在，求出正整数n，t；若不存在，说明理由．

10．

市体育运动学校的甲、乙两名篮球运动员练习投篮，每人练习10次，每次投篮40个．命中个数的茎叶图如下．则投篮命中率较高的运动员是甲．

17．等差数列{a_n}前n项和为S_n，且6S₅-5S₃=5，a₂=1，则S_n的最大值为$\frac{10}{3}$．

7．已知一次函数满足f（f（x））=4x+1，则解析式f（x）=2x$+\frac{1}{3}$，或-2x-1．

14．集合N={x||x|≤1，x∈R}，M={x|x≤0，x∈R}，则M∩N=（　　）

11．等比数列{a_n}的各项均为正数，且a₅a₆+a₄a₇=18，则log₃a₁+log₃a₂+…+log₃a₁₀=（　　）

log₃45

12．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x-1），x＞1}\\{{3}^{x}+2，x≤1}\end{array}\right.$则f（f（log₃2））的值是（　　）

1+log₃2

试题分类