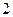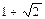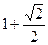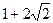题目内容
将圆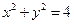 上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。
上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。
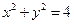 上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。
上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。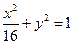
设所得曲线上任一点坐标为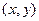 ,圆
,圆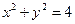 上的对应点的坐标为
上的对应点的坐标为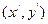 ,则由题意可得
,则由题意可得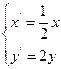 ,因为
,因为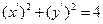 ,所以
,所以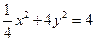 ,即
,即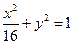 。这就是变换后所得的曲线的方程,它表示一个椭圆。
。这就是变换后所得的曲线的方程,它表示一个椭圆。
名师点金:原题是保持横坐标不变,纵坐标变为原来的一半,所得的是焦点在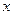 轴上的椭圆,变式中保持纵坐标不变,横坐标变为原来的一半,所得的是焦点在
轴上的椭圆,变式中保持纵坐标不变,横坐标变为原来的一半,所得的是焦点在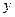 轴上的椭圆,另外,本题的变式还有很多,如:横坐标与纵坐标同时缩小、同时扩大及一个缩小而另一个扩大等。
轴上的椭圆,另外,本题的变式还有很多,如:横坐标与纵坐标同时缩小、同时扩大及一个缩小而另一个扩大等。
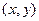 ,圆
,圆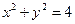 上的对应点的坐标为
上的对应点的坐标为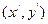 ,则由题意可得
,则由题意可得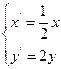 ,因为
,因为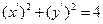 ,所以
,所以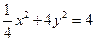 ,即
,即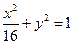 。这就是变换后所得的曲线的方程,它表示一个椭圆。
。这就是变换后所得的曲线的方程,它表示一个椭圆。名师点金:原题是保持横坐标不变,纵坐标变为原来的一半,所得的是焦点在
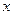 轴上的椭圆,变式中保持纵坐标不变,横坐标变为原来的一半,所得的是焦点在
轴上的椭圆,变式中保持纵坐标不变,横坐标变为原来的一半,所得的是焦点在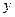 轴上的椭圆,另外,本题的变式还有很多,如:横坐标与纵坐标同时缩小、同时扩大及一个缩小而另一个扩大等。
轴上的椭圆,另外,本题的变式还有很多,如:横坐标与纵坐标同时缩小、同时扩大及一个缩小而另一个扩大等。
练习册系列答案
相关题目
 和B
和B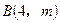 并且与
并且与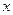 轴相切的圆有且只有一个,求实数
轴相切的圆有且只有一个,求实数 的值和这个圆的方程。
的值和这个圆的方程。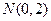 ,且与定直线
,且与定直线 相切.
相切.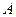 、
、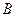 是轨迹C上的两不同动点,且
是轨迹C上的两不同动点,且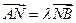 . 分别以
. 分别以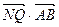 为定值.
为定值. 围成的图形的面积。
围成的图形的面积。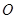 引圆
引圆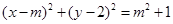 的切线
的切线 ,当
,当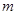 变化时,切点
变化时,切点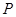 的轨迹方程是( )
的轨迹方程是( )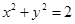

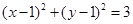
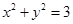
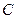 和
和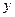 轴相切,圆心在直线
轴相切,圆心在直线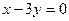 上,且被直线
上,且被直线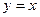 截得的弦长为
截得的弦长为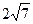
 ,求圆
,求圆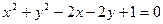 上的点到直线
上的点到直线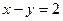 的距离最大值是( )
的距离最大值是( )