题目内容
已知曲线C:x2+y2+2kx+(4k+10)y+10k+20=0,其中k≠-1.
(1)求证:曲线C都表示圆,并且这些圆心都在同一条直线上;
(2)证明:曲线C过定点;
(3)若曲线C与x轴相切,求k的值.
(1)求证:曲线C都表示圆,并且这些圆心都在同一条直线上;
(2)证明:曲线C过定点;
(3)若曲线C与x轴相切,求k的值.
(1)圆的圆心都在直线2x-y-5=0上. (2)曲线C过定点(1,-3). (3) .
.
 .
. (1)原方程可化为(x+k)2+(y+2k+5)2=5(k+1)2.
∵k≠-1,?
∴5(k+1)2>0.?
故方程表示圆心为(-k,-2k-5),
半径为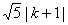 的圆.
的圆.
设圆心为(x,y),有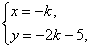
消去k,得2x-y-5=0.?
∴这些圆的圆心都在直线2x-y-5=0上.
(2)将原方程变形成?
k(2x+4y+10)+(x2+y2+10y+20)=0.?
上式关于参数k是恒等式,?
∴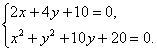
解得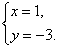
∴曲线C过定点(1,-3).
(3)∵圆C与x轴相切,
∴圆心到x轴的距离等于半径,
即|-2k-5|= |k+1|.?
|k+1|.?
两边平方,得(2k+5)2=5(k+1)2.
∴ .
.
∵k≠-1,?
∴5(k+1)2>0.?
故方程表示圆心为(-k,-2k-5),
半径为
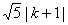 的圆.
的圆.设圆心为(x,y),有
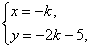
消去k,得2x-y-5=0.?
∴这些圆的圆心都在直线2x-y-5=0上.
(2)将原方程变形成?
k(2x+4y+10)+(x2+y2+10y+20)=0.?
上式关于参数k是恒等式,?
∴
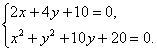
解得
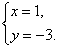
∴曲线C过定点(1,-3).
(3)∵圆C与x轴相切,
∴圆心到x轴的距离等于半径,
即|-2k-5|=
 |k+1|.?
|k+1|.?两边平方,得(2k+5)2=5(k+1)2.
∴
 .
.
练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目


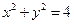 上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。
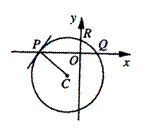
上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。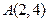 向圆
向圆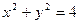 所引的切线方程
所引的切线方程
 与圆
与圆 的位置关系是( ).
的位置关系是( ).