题目内容
已知动圆过定点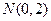 ,且与定直线
,且与定直线 相切.
相切.
(1)求动圆圆心的轨迹C的方程;
(2)若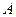 、
、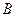 是轨迹C上的两不同动点,且
是轨迹C上的两不同动点,且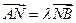 . 分别以
. 分别以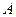 、
、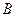 为切点作轨迹C的切线,设其交点Q,证明
为切点作轨迹C的切线,设其交点Q,证明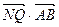 为定值.
为定值.
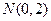 ,且与定直线
,且与定直线 相切.
相切.(1)求动圆圆心的轨迹C的方程;
(2)若
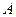 、
、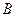 是轨迹C上的两不同动点,且
是轨迹C上的两不同动点,且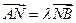 . 分别以
. 分别以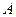 、
、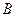 为切点作轨迹C的切线,设其交点Q,证明
为切点作轨迹C的切线,设其交点Q,证明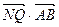 为定值.
为定值.(1)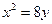 ;(2)0
;(2)0
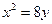 ;(2)0
;(2)0解:(1)依题意,圆心的轨迹是以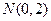 为焦点,
为焦点, 为准线的抛物线上
为准线的抛物线上
因为抛物线焦点到准线距离等于4 所以圆心的轨迹是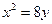
(2)由已知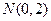 ,设
,设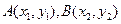 ,由
,由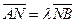 ,
,
即得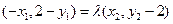 ,故
,故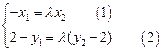
将(1)式两边平方并把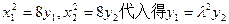 (3)
(3)
解(2)、(3)式得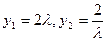 ,且有
,且有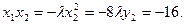
抛物线方程为 所以过抛物线上A、B两点的切线方程分别是
所以过抛物线上A、B两点的切线方程分别是
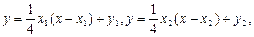
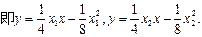

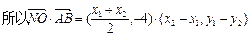
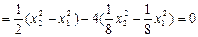
所以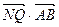 为定值,其值为0.
为定值,其值为0.
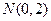 为焦点,
为焦点, 为准线的抛物线上
为准线的抛物线上因为抛物线焦点到准线距离等于4 所以圆心的轨迹是
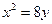
(2)由已知
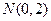 ,设
,设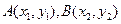 ,由
,由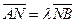 ,
,即得
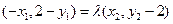 ,故
,故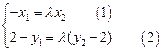
将(1)式两边平方并把
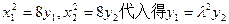 (3)
(3)解(2)、(3)式得
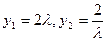 ,且有
,且有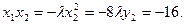
抛物线方程为
 所以过抛物线上A、B两点的切线方程分别是
所以过抛物线上A、B两点的切线方程分别是 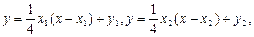
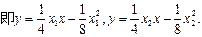

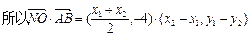
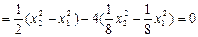
所以
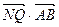 为定值,其值为0.
为定值,其值为0. 
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
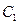 :
: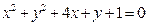 及
及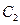 :
: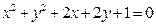 的公共弦为直径的圆的方程.
的公共弦为直径的圆的方程.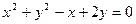
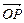 ·
· =0.
=0.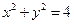 上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。
上的点的横坐标变为原来的2倍,纵坐标变为原来的一半,求所得曲线的方程。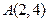 向圆
向圆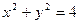 所引的切线方程
所引的切线方程
 与圆
与圆 的位置关系是( ).
的位置关系是( ).